练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （12分）若，，函数图象对称中心到对称轴最小距离为，当时f(x)的最大值为1.（1）求f(x)解析式；（2）若，，求x的值.

    （1）（2）或


    解析:

    （1）∵，

    ∴

    ，

    又∵，∴T=π，.∴.

    又，∴，∴，∴f(x)∈[t,3+t]，又f(x)max=1, ∴3+t=1，故t=-1.∴.

    （2）∵，∴.∵，得，∴ 或，∴或.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    复数z1=sinx+i，z2=1+i•cosx（x∈R）在坐标平面中对应的点分别是A，B，若函数f（x）=
    OA
    •
    OB
    （O为坐标原点），则下列命题正确的是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知定义在区间[-π，
    3π
    2
    ]    上的函数y=f（x）图象关于直线x=
    π
    4
    对称，当x≥
    π
    4
    时，f（x）=-sinx．
    （1）作出y=f（x）的图象；
    （2）求y=f（x）的解析式；
    （3）若关于x的方程f(x)=-
    9
    10
    有解，将方程所有的解的和记为M，结合（1）中函数图象，求M的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某校高一年级数学兴趣小组的同学经过研究，证明了以下两个结论是完全正确的：①若函数y=f（x）的图象关于点P（a，b）成中心对称图形，则函数y=f（x+a）-b是奇函数；②若函数y=f（x+a）-b是奇函数，则函数y=f（x）的图象关于点P（a，b）成中心对称图形．请你利用他们的研究成果完成下列问题：
    （1）将函数g（x）=x3+6x2的图象向右平移2个单位，再向下平移16个单位，求此时图象对应的函数解释式，并利用已知条件中的结论求函数g（x）图象对称中心的坐标；
    （2）求函数h(x)=log2
    1-x4x
    图象对称中心的坐标，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （1）在学习函数的奇偶性时我们知道：若函数y=f（x）的图象关于点P（0，0）成中心对称图形，则有函数y=f（x）为奇函数，反之亦然；现若有函数y=f（x）的图象关于点P（a，b）成中心对称图形，则有与y=f（x）相关的哪个函数为奇函数，反之亦然．
    （2）将函数g（x）=x3+6x2的图象向右平移2个单位，再向下平移16个单位，求此时图象对应的函数解释式，并利用（1）的性质求函数g（x）图象对称中心的坐标；
    （3）利用（1）中的性质求函数h（x）=log2
    1-x4x
    图象对称中心的坐标，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源：安徽省模拟题 题型：填空题

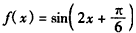    已知下列命题：①已知α，β表示两个不同的平面，m为平面α内的一条直线，则“α⊥β”是“m⊥β”的充要条件；
    ②函数图象对称中心的坐标为；
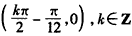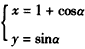    ③在平面直角坐标系中圆C的参数方程为（α为参数），若以原点为极点，x轴非负半轴为极轴，则圆C的极坐标方程为ρ=2cosθ；
    ④在△ABC中，若b=2asinB(其中a，b分别为角A，角B的对边)，则A等于30°；
    其中真命题的序号是（    ）（填上所有正确的序号）。

    查看答案和解析>>

    同步练习册答案