
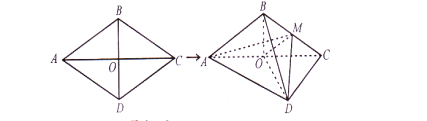
【题目】如图,菱形![]() 的边长为
的边长为![]() ,
,![]() ,
,![]() 与
与![]() 交于
交于![]() 点.将菱形
点.将菱形![]() 沿对角线
沿对角线![]() 折起,得到三棱锥
折起,得到三棱锥![]() ,点
,点![]() 是棱
是棱![]() 的中点,
的中点,![]() .
.
(I)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(II)求二面角![]() 的余弦值.
的余弦值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为![]() (t为参数),以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ(ρ﹣2sinθ)=1.
(t为参数),以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ(ρ﹣2sinθ)=1.
(1)求C的直角坐标方程;
(2)设直线l与y轴相交于P,与曲线C相交于A、B两点,且|PA|+|PB|=2,求点O到直线l的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为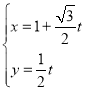 (t为参数),在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρsin2θ=4cosθ.
(t为参数),在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρsin2θ=4cosθ.
(1)求直线l的普通方程与曲线C的直角坐标方程;
(2)若直线l与x轴的交点为F,直线l与曲线C的交点为A、B,求|FA|+|FB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程:在直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)已知点![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,它与曲线
,它与曲线![]() 的交点为
的交点为![]() ,
,![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将边长为1的正方形ABCD沿x轴正向滚动,先以A为中心顺时针旋转,当B落在x轴时,又以B为中心顺时针旋转,如此下去,设顶点C滚动时的曲线方程为![]() ,则下列说法不正确的是
,则下列说法不正确的是![]()

A.![]() 恒成立B.
恒成立B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)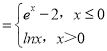 ,g(x)=f(
,g(x)=f(![]() )+1(k∈R,k≠0),则下列关于函数y=f[g(x)]+1的零点个数判断正确的是( )
)+1(k∈R,k≠0),则下列关于函数y=f[g(x)]+1的零点个数判断正确的是( )
A.当k>0时,有2个零点;当k<0时,有4个零点
B.当k>0时,有4个零点;当k<0时,有2个零点
C.无论k为何值,均有2个零点
D.无论k为何值,均有4个零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2011年国际数学协会正式宣布,将每年的3月14日设为国际数学节,来源于中国古代数学家祖冲之的圆周率。公元263年,中国数学家刘徽用“割圆术”计算圆周率,计算到圆内接3072边形的面积,得到的圆周率是![]() .公元480年左右,南北朝时期的数学家祖冲之进一步得出精确到小数点后7位的结果,给出不足近似值3.1415926和过剩近似值3.1415927,还得到两个近似分数值,密率
.公元480年左右,南北朝时期的数学家祖冲之进一步得出精确到小数点后7位的结果,给出不足近似值3.1415926和过剩近似值3.1415927,还得到两个近似分数值,密率![]() 和约率
和约率![]() 。大约在公元530年,印度数学大师阿耶波多算出圆周率约为
。大约在公元530年,印度数学大师阿耶波多算出圆周率约为![]() (
(![]() ).在这4个圆周率的近似值中,最接近真实值的是( )
).在这4个圆周率的近似值中,最接近真实值的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com