
【题目】某市教育局委托调查机构对本市中小学学校使用“微课掌上通”满意度情况进行调查.随机选择小学和中学各50所学校进行调查,调查情况如表:
评分等级 | ☆ | ☆☆ | ☆☆☆ | ☆☆☆☆ | ☆☆☆☆☆ |
小学 | 2 | 7 | 9 | 20 | 12 |
中学 | 3 | 9 | 18 | 12 | 8 |
(备注:“☆”表示评分等级的星级,例如“☆☆☆”表示3星级.)
(1)从评分等级为5星级的学校中随机选取两所学校,求恰有一所学校是中学的概率;
(2)规定:评分等级在4星级以上(含4星)为满意,其它星级为不满意.完成下列2×2列联表并帮助判断:能否在犯错误的概率不超过0.05的前提下认为使用是否满意与学校类别有关系?
学校类型 | 满意 | 不满意 | 总计 |
小学 | 50 | ||
中学 | 50 | ||
总计 | 100 |
【答案】
(1)解:因为从5星级的20所学校中随机选取2所,共有 ![]() =190种结果,
=190种结果,
其中恰有1所学校是中学的共有 ![]()
![]() =96种结果,;
=96种结果,;
故所求概率为P= ![]() =
= ![]()
(2)解:由2×2列联表:
学校类型 | 满意 | 不满意 | 总计 |
小学 | 32 | 18 | 50 |
中学 | 20 | 30 | 50 |
总计 | 52 | 48 | 100 |
经计算K2的观测值:K2= ![]() ≈5.769>3.841;
≈5.769>3.841;
所以在犯错误的概率不超过0.05的前提下认为使用满意与学校类型有关系.
【解析】(1)由古典概型公式,分别求得从5星级的20所学校中随机选取2所总事件个数m及恰有1所学校是中学的事件个数n,P= ![]() =
= ![]() ,代入即可求得x和y的值;(2)根据所给数据,可得2×2列联表,求出K2 , 与临界值比较,在犯错误的概率不超过0.05的前提下认为使用满意与学校类型有关系.
,代入即可求得x和y的值;(2)根据所给数据,可得2×2列联表,求出K2 , 与临界值比较,在犯错误的概率不超过0.05的前提下认为使用满意与学校类型有关系.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+b满足f(1)=0,且在x=2时函数取得极值.
(1)求a,b的值;
(2)求函数f(x)的单调区间;
(3)求函数f(x)在区间[0,t](t>0)上的最大值g(t)的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=ax3﹣x2+cx(a≠0)的图象如图所示,它与x轴仅有两个公共点O(0,0)与A(xA , 0)(xA>0); 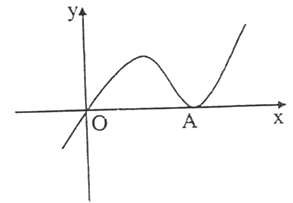
(1)用反证法证明常数c≠0;
(2)如果 ![]() ,求函数的解析式.
,求函数的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某产品的历史收益率的频率分布直方图如图所示:
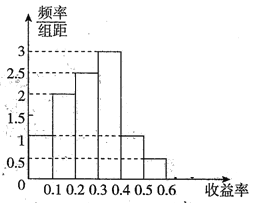
(1)试计算该产品收益率的中位数;
(2)若该产品的售价![]() (元)与销量
(元)与销量![]() (万件)之间有较强线性相关关系,从历史销售记录中抽样得到如表5组
(万件)之间有较强线性相关关系,从历史销售记录中抽样得到如表5组![]() 与
与![]() 的对应数据:
的对应数据:
售价 | 25 | 30 | 38 | 45 | 52 |
销量 | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
据此计算出的回归方程为![]() ,求
,求![]() 的值;
的值;
(3)若从上述五组销量中随机抽取两组,求两组销量中恰有一组超过6万件的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 在点(1,2)处的切线与f(x)的图象有三个公共点,则b的取值范围是( )
在点(1,2)处的切线与f(x)的图象有三个公共点,则b的取值范围是( )
A.[﹣8,﹣4+2 ![]() )
)
B.(﹣4﹣2 ![]() ,﹣4+2
,﹣4+2 ![]() )
)
C.(﹣4+2 ![]() ,8]
,8]
D.(﹣4﹣2 ![]() ,﹣8]
,﹣8]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对甲、乙的学习成绩进行抽样分析,各抽五门功课,得到的观测值如表:
甲 | 60 | 80 | 70 | 90 | 70 |
乙 | 80 | 60 | 70 | 80 | 75 |
问:甲、乙谁的平均成绩较好?谁的各门功课发展较平衡?( )
A.甲的平均成绩较好,乙的各门功课发展较平衡
B.甲的平均成绩较好,甲的各门功课发展较平衡
C.乙的平均成绩较好,甲的各门功课发展较平衡
D.乙的平均成绩较好,乙的各门功课发展较平衡
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,将曲线
中,将曲线![]() 上的所有点横坐标伸长为原来的
上的所有点横坐标伸长为原来的![]() 倍,纵坐标伸长为原来的2倍后,得到曲线
倍,纵坐标伸长为原来的2倍后,得到曲线![]() ,在以
,在以![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出曲线![]() 的参数方程和直线
的参数方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)在曲线![]() 上求一点
上求一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离
的距离![]() 最大,并求出此最大值.
最大,并求出此最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣ ![]() x2+(a﹣1)x+lnx.
x2+(a﹣1)x+lnx.
(1)若a>﹣1,求函数f(x)的单调区间;
(2)若g(x)= ![]() x2+(1﹣2a)x+f(x)有且只有两个零点,求实数a的取值范围.
x2+(1﹣2a)x+f(x)有且只有两个零点,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com