
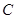 :
: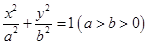 的离心率为
的离心率为 ,
,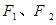 分别为椭圆
分别为椭圆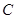 的左、右焦点,若椭圆
的左、右焦点,若椭圆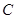 的焦距为2.
的焦距为2.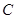 的方程;
的方程;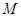 为椭圆上任意一点,以
为椭圆上任意一点,以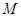 为圆心,
为圆心, 为半径作圆
为半径作圆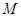 ,当圆
,当圆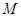 与椭圆的右准线
与椭圆的右准线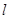 有公共点时,求△
有公共点时,求△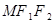 面积的最大值.
面积的最大值. .⑵
.⑵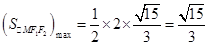 .
. 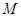 与
与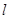 有公共点,所以
有公共点,所以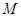 到
到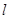 的距离
的距离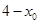 小于或等于圆的半径
小于或等于圆的半径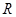 .因为
.因为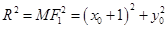 ,所以
,所以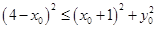 ,
, .然后再借助椭圆方程,消y0转化为
.然后再借助椭圆方程,消y0转化为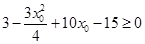 求解即可。
求解即可。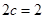 ,且
,且 ,所以
,所以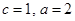 .……………………………………2分
.……………………………………2分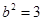 .………………………………………………………………………………4分
.………………………………………………………………………………4分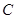 的方程为
的方程为 .……………………………………………………6分
.……………………………………………………6分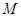 的坐标为
的坐标为 ,则
,则 .
.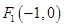 ,
,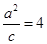 ,所以直线
,所以直线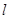 的方程为
的方程为 .………………………………8分
.………………………………8分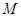 与
与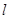 有公共点,所以
有公共点,所以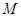 到
到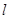 的距离
的距离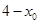 小于或等于圆的半径
小于或等于圆的半径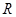 .
.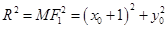 ,所以
,所以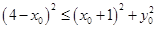 ,………………10分
,………………10分 .
. ,所以
,所以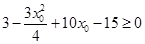 .…………………………12分
.…………………………12分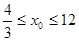 ,又
,又 ,∴
,∴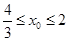 .……………………………………14分
.……………………………………14分 时,
时, ,所以
,所以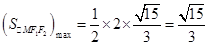 .…………16分
.…………16分

 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源:不详 题型:解答题
 ,过左焦点
,过左焦点 作直线
作直线 与椭圆交于点P,Q,直线AP,AQ分别与直线
与椭圆交于点P,Q,直线AP,AQ分别与直线 交于点
交于点 .
. 为直径的圆经过焦点
为直径的圆经过焦点 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
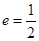 ,过左焦点
,过左焦点 作直线
作直线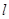 与椭圆交于点P,Q,直线AP,AQ分别与直线
与椭圆交于点P,Q,直线AP,AQ分别与直线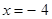 交于点
交于点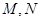 .
.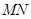 为直径的圆经过焦点
为直径的圆经过焦点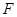 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的离心率为
的离心率为 ,且过点Q(1,
,且过点Q(1, ).
).
 (O为坐标原点),求实数t的最小值.
(O为坐标原点),求实数t的最小值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,直线
,直线 过椭圆左焦点
过椭圆左焦点 且不与
且不与 轴重合,
轴重合,  与椭圆交于
与椭圆交于 ,两点,当
,两点,当 与
与 轴垂直时,
轴垂直时, ,若点
,若点 且
且
 的方程;
的方程; 绕着
绕着 旋转,与圆
旋转,与圆 交于
交于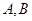 两点,若
两点,若 ,求
,求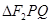 的面积
的面积 的取值范围(
的取值范围( 为椭圆的右焦点)。
为椭圆的右焦点)。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,
,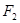 是椭圆
是椭圆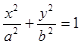
 左右焦点,它的离心率
左右焦点,它的离心率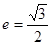 ,且被直线
,且被直线 所截得的线段的中点的横坐标为
所截得的线段的中点的横坐标为
 是其椭圆上的任意一点,当
是其椭圆上的任意一点,当 为钝角时,求
为钝角时,求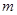 的取值范围。
的取值范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 的左、右焦点,点P在椭圆上,且
的左、右焦点,点P在椭圆上,且 记线段PF1与y轴的交点为Q,O为坐标原点,若△F1OQ与四边形OF2PQ的面积之比为1: 2,则该椭圆的离心率等于 ( )
记线段PF1与y轴的交点为Q,O为坐标原点,若△F1OQ与四边形OF2PQ的面积之比为1: 2,则该椭圆的离心率等于 ( )A.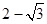 | B.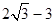 | C. | D.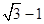 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com