
【题目】如图,在锐角△ABC中,AB=AC,∠ACB的平分线与AB交于点D,过△ABC的外心O作CD的垂线与AC交于点E,过E作AB的平行线与CD交于点F。证明:

(1)C、E、0、F四点共圆;
(2)A、0、F三点共线;
(3)EA=EF。
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】
(1)如图,联结0C、0A、OF.因为AB=AC,0为△ABC的外心,所以,0A平分∠BAC,OA =0C.

则![]() .
.
由OE⊥CD,CD平分∠ACB,知∠OEC=90°-∠ECD![]() .
.
则![]() .
.
又由EF//AD,CD平分∠ACB,知∠CFE=∠CDA=∠ABC+∠DCB=![]() .
.
故∠CFE=∠EOC.
因此,C、E、0、F四点共圆.
(2)由0为△ABC的外心,知∠AOC=2∠B.
因为C、E、O、F四点共圆,所以,∠FOC=∠FEC=∠BAC.
故∠FOC+∠AOC=∠BAC+2∠B=180°.
因此,A、O、F三点共线.
(3)由C、E、0、F四点共圆知∠0FE=∠OCE=∠OAC.
从而,EA=EF.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为F1,F2,过点F1的直线与C交于A,B两点.△ABF2的周长为
的左、右焦点分别为F1,F2,过点F1的直线与C交于A,B两点.△ABF2的周长为![]() ,且椭圆的离心率为
,且椭圆的离心率为![]() .
.
(1)求椭圆C的标准方程:
(2)设点P为椭圆C的下顶点,直线PA,PB与y=2分别交于点M,N,当|MN|最小时,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以坐标原点为中心,以坐标轴为对称轴的帮圆C经过点M(2,1),N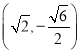 .
.
(1)求椭圆C的标准方程;
(2)经过点M作倾斜角互补的两条直线,分别与椭圆C相交于异于M点的A,B两点,当△AMB面积取得最大值时,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
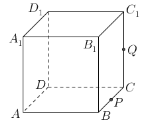
【题目】如图,正方体![]() 的棱长为1,
的棱长为1,![]() 为
为![]() 的中点,
的中点,![]() 为线段
为线段![]() 上的动点,过点
上的动点,过点![]()
![]()
![]() 的平面截该正方体所得的截面记为
的平面截该正方体所得的截面记为![]() ,给出下列三个结论:
,给出下列三个结论:
① 当![]() 时,
时,![]() 为四边形;
为四边形;
② 当![]() 时,
时,![]() 为等腰梯形;
为等腰梯形;
③ 当![]() 时,
时,![]() 的面积为
的面积为![]() ;
;
以上结论正确的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义空间点到几何图形的距离为:这一点到这个几何图形上各点距离中最短距离.
(1)在空间,求与定点![]() 距离等于1的点所围成的几何体的体积和表面积;
距离等于1的点所围成的几何体的体积和表面积;
(2)在空间,线段![]() (包括端点)的长等于1,求到线段
(包括端点)的长等于1,求到线段![]() 的距离等于1的点所围成的几何体的体积和表面积;
的距离等于1的点所围成的几何体的体积和表面积;
(3)在空间,记边长为1的正方形![]() 区域(包括边界及内部的点)为
区域(包括边界及内部的点)为![]() ,求到
,求到![]() 距离等于1的点所围成的几何体的体积和表面积.
距离等于1的点所围成的几何体的体积和表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(m2-m-1)x-5m-3,m为何值时,f(x):
(1)是幂函数;
(2)是正比例函数;
(3)是反比例函数;
(4)是二次函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在研究吸烟与患肺癌的关系中,通过收集数据、整理分析数据得“吸烟与患肺癌有关”的结论,并且在犯错误的概率不超过0.01的前提下认为这个结论是成立的,下列说法中正确的是( )
A.100个吸烟者中至少有99人患有肺癌
B.1个人吸烟,那么这个人有99%的概率患有肺癌
C.在100个吸烟者中一定有患肺癌的人
D.在100个吸烟者中可能一个患肺癌的人也没有
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com