
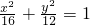 ,双曲线C2与C1具有相同的焦点,且离心率互为倒数.
,双曲线C2与C1具有相同的焦点,且离心率互为倒数. (a>0,b>0)
(a>0,b>0) ,焦点为F(±2,0),
,焦点为F(±2,0),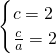 ,
,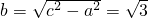 .
.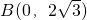 ,双曲线C2的顶点为M(±1,0),椭圆C1与双曲线C2的交点为N(±2,±3),
,双曲线C2的顶点为M(±1,0),椭圆C1与双曲线C2的交点为N(±2,±3),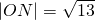 .
.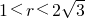 或
或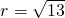 或r>4.
或r>4. ,
,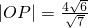 ,
,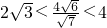 ,且
,且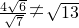 ,
,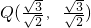 ,
,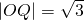 ,
,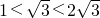 ,符合要求,
,符合要求,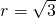 时,交点有且仅有四个,顺次连接这四个交点所得到的四边形是正方形.
时,交点有且仅有四个,顺次连接这四个交点所得到的四边形是正方形. (a>0,b>0),由双曲线C2与C1具有相同的焦点,且离心率互为倒数,知
(a>0,b>0),由双曲线C2与C1具有相同的焦点,且离心率互为倒数,知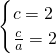 ,由此可求出双曲线C2的方程.
,由此可求出双曲线C2的方程.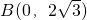 ,双曲线C2的顶点为M(±1,0),椭圆C1与双曲线C2的交点为N(±2,±3),
,双曲线C2的顶点为M(±1,0),椭圆C1与双曲线C2的交点为N(±2,±3),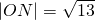 .所以圆C与两曲线C1、C2有且仅有四个交点,再运用曲线的对称性将问题转化从而简化计算.
.所以圆C与两曲线C1、C2有且仅有四个交点,再运用曲线的对称性将问题转化从而简化计算.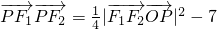 ,则动点轨迹也是曲线C2.
,则动点轨迹也是曲线C2. 

 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源:2012-2013学年贵州省六校联盟高三(上)第一次联考数学试卷(文科)(解析版) 题型:选择题
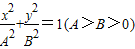 和双曲线C2:
和双曲线C2: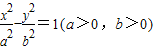 有相同的焦点F1、F2,2c是它们的共同焦距,且它们的离心率互为倒数,P是它们在第一象限的交点,当cos∠F1PF2=60°时,下列结论中正确的是( )
有相同的焦点F1、F2,2c是它们的共同焦距,且它们的离心率互为倒数,P是它们在第一象限的交点,当cos∠F1PF2=60°时,下列结论中正确的是( )查看答案和解析>>
科目:高中数学 来源:2008-2009学年河北省衡水市中学高二(上)第二次调研数学试卷(解析版) 题型:解答题
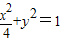 ,双曲线C2:
,双曲线C2: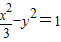 .若直线
.若直线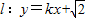 与椭圆C1、双曲线C2都恒有两个不同的交点,且l与C2的两交点A、B满足
与椭圆C1、双曲线C2都恒有两个不同的交点,且l与C2的两交点A、B满足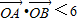 (其中O为原点),求k的取值范围.
(其中O为原点),求k的取值范围.查看答案和解析>>
科目:高中数学 来源:2010年广东省江门市高考数学后阶段备考指导和猜题试卷(解析版) 题型:解答题
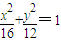 ,双曲线C2与C1具有相同的焦点,且离心率互为倒数.
,双曲线C2与C1具有相同的焦点,且离心率互为倒数.查看答案和解析>>
科目:高中数学 来源:2011年高考数学综合复习试卷(2)(解析版) 题型:解答题
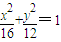 ,双曲线C2与C1具有相同的焦点,且离心率互为倒数.
,双曲线C2与C1具有相同的焦点,且离心率互为倒数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com