练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列从总体中抽得的样本是否为简单随机样本？

    （1）总体编号为1~75.在0~99中产生随机整数r.若或.则舍弃，重新抽取.

    （2）总体编号为1~75.在0~99中产生随机整数r，r除以75的余数作为抽中的编号，若余数为0.则抽中75.

    （3）总体编号为6001~6876.在1~876范围内产生一个随机整数r，把r+6000作为抽中的编号.

    【答案】（1）不是简单随机样本；（2）不是简单随机样本；（3）是简单随机样本.

    【解析】

    根据抽中的可能性是否相等依次判断每个选项得到答案.

    （1）总体编号为1~75.在0~99中产生随机整数r.若或.则舍弃，重新抽取.

    只有编号为1~75可能被抽中，故不是等可能性的，不是简单随机抽样；

    （2）总体编号为1~75.在0~99中产生随机整数r，r除以75的余数作为抽中的编号，若余数为0.则抽中75.

    1~24,75号与25~74号抽中的可能性不同，故不是简单随机抽样；

    （3）总体编号为6001~6876.在1~876范围内产生一个随机整数r，把r+6000作为抽中的编号.

    每个编号抽中的可能性相同，是简单随机抽样；

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】2019年，随着中国第一款5G手机投入市场，5G技术已经进入高速发展阶段.已知某5G手机生产厂家通过数据分析，得到如下规律：每生产手机万台，其总成本为，其中固定成本为800万元，并且每生产1万台的生产成本为1000万元（总成本=固定成本+生产成本），销售收入万元满足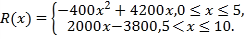

    （1）将利润表示为产量万台的函数；

    （2）当产量为何值时，公司所获利润最大？最大利润为多少万元？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设 的内角 的对边分别为 已知 ．

    （1）求角 ；

    （2）若 ， ，求 的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）判断函数的奇偶性，并说明理由；

    （2）设，问函数的图像是否关于某直线成轴对称图形，如果是，求出的值，如果不是，请说明理由；（可利用真命题：“函数的图像关于某直线成轴对称图形”的充要条件为“函数是偶函数”）

    （3）设，函数，若函数与的图像有且只有一个公共点，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】太极图是由黑白两个鱼形纹组成的图案，俗称阴阳鱼，太极图展现了一种相互转化，相对统一的和谐美，定义：能够将圆的周长和面积同时等分成两个部分的函数称为圆的一个“太极函数”，则下列有关说法中：

    ①对于圆的所有非常数函数的太极函数中，都不能为偶函数；

    ②函数是圆的一个太极函数；

    ③直线所对应的函数一定是圆的太极函数；

    ④若函数是圆的太极函数，则

    所有正确的是__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

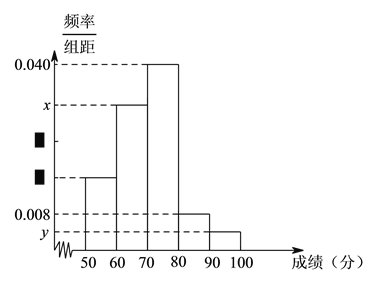
    【题目】某中学举行一次“环保知识竞赛”，全校学生参加了这次竞赛．为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取正整数，满分为分）作为样本进行统计，请根据下面尚未完成并有局部污损的样本的频率分布表和频率分布直方图（如图所示）解决下列问题：

    （Ⅰ）写出， ， ， 的值．

    （Ⅱ）在选取的样本中，从竞赛成绩是分以上（含分）的同学中随机抽取名同学到广场参加环保知识的志愿宣传活动，求所抽取的名同学来自同一组的概率．

    （Ⅲ）在（Ⅱ）的条件下，设表示所抽取的名同学中来自第组的人数，求的分布列及其数学期望．

    组别

    分组

    频数

    频率

    第组

    第组

    第组

    第组

    第组

    合计

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知曲线C1：，曲线C2：．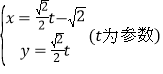

    （1）指出C1，C2各是什么曲线，并说明C1与C2公共点的个数；

    （2）若把C1，C2上各点的纵坐标都压缩为原来的一半，分别得到曲线，．写出，的参数方程．与公共点的个数和C1与C2公共点的个数是否相同？说明你的理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，函数．

    （1）当时，求函数在上的最值；

    （2）若函数在上单调递增，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着资本市场的强势进入，互联网共享单车“忽如一夜春风来”，遍布了一二线城市的大街小巷.为了解共享单车在市的使用情况，某调查机构借助网络进行了问卷调查，并从参与调查的网友中随机抽取了200人进行抽样分析，得到下表（单位：人）：

    经常使用

    偶尔或不用

    合计

    30岁及以下

    70

    30

    100

    30岁以上

    60

    40

    100

    合计

    130

    70

    200

    （1）根据以上数据，能否在犯错误的概率不超过0.15的前提下认为市使用共享单车情况与年龄有关？

    （2）现从所有抽取的30岁以上的网民中利用分层抽样抽取5人，

    求这5人中经常使用、偶尔或不用共享单车的人数；

    从这5人中，在随机选出2人赠送一件礼品，求选出的2人中至少有1人经常使用共享单车的概率.

    参考公式： ，其中.

    （）

    0.15

    0.10

    0.05

    0.025

    0.010

    2.072

    2.706

    3.841

    5.024

    6.635

    查看答案和解析>>

    同步练习册答案