
【题目】已知椭圆![]() +y2=1上两个不同的点A,B关于直线y=mx+
+y2=1上两个不同的点A,B关于直线y=mx+![]() 对称.
对称.
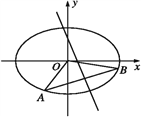
(1)求实数m的取值范围;
(2)求△AOB面积的最大值(O为坐标原点).
【答案】(1)m<-![]() 或m>
或m>![]() .(2)
.(2)![]()
【解析】试题分析:(1)设直线![]() 的方程为
的方程为![]() ,代入椭圆方程消去
,代入椭圆方程消去![]() ,设
,设![]() ,可得
,可得![]() ,设线段
,设线段![]() 的中点
的中点![]() ,利用中点坐标公式及其根与系数的可得
,利用中点坐标公式及其根与系数的可得![]() ,代入直线
,代入直线![]() ,可得
,可得![]() ,代入
,代入![]() ,即可解出
,即可解出![]() 的范围;(2)结合(1),
的范围;(2)结合(1),![]() 换元后根据韦达定理、弦长公式、点到直线距离公式,利用三角形面积公式,将三角形面积用
换元后根据韦达定理、弦长公式、点到直线距离公式,利用三角形面积公式,将三角形面积用![]() 表示,再利用二次函数配方法即可得出三角形面积的最大值.
表示,再利用二次函数配方法即可得出三角形面积的最大值.
试题解析: (1) 由题意知m≠0,
可设直线AB的方程为y=-![]() x+b.
x+b.
由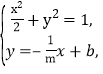 消去y,得
消去y,得![]() +
+![]() x2-
x2-![]() x+b2-1=0.
x+b2-1=0.
因为直线y=-![]() x+b与椭圆
x+b与椭圆![]() +y2=1有两个不同的交点, 所以Δ=-2b2+2+
+y2=1有两个不同的交点, 所以Δ=-2b2+2+![]() >0,①
>0,①
将线段AB中点M(![]() ,
,![]() )代入直线方程y=mx+
)代入直线方程y=mx+![]() ,解得b=-
,解得b=-![]() .②
.②
由①②得m<-![]() 或m>
或m>![]() .
.
(2)令t=![]() ∈(-
∈(-![]() ,0)∪(0,
,0)∪(0,![]() ),
),
则|AB|=![]() ·
·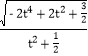 ,
,
且O到直线AB的距离为d=![]() .
.
设△AOB的面积为S(t),
所以S(t)=![]() |AB|·d=
|AB|·d=![]() ≤
≤![]() .
.
当且仅当t2=![]() 时,等号成立.
时,等号成立.
故△AOB面积的最大值为![]() .
.
【方法点晴】本题主要考查直线与椭圆的位置关系及圆锥曲线求最值,属于难题.解决圆锥曲线中的最值问题一般有两种方法:一是几何意义,特别是用圆锥曲线的定义和平面几何的有关结论来解决,非常巧妙;二是将圆锥曲线中最值问题转化为函数问题,然后根据函数的特征选用参数法、配方法、判别式法、三角函数有界法、函数单调性法以及均值不等式法,本题(2)就是用的这种思路,利用配方法法求三角形面积最值的.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,底面ABCD是一直角梯形,BA⊥AD,AD∥BC,AB=BC=2,PA=3,PA⊥底面ABCD,E是棱PD上异于P,D的动点.设 ![]() =m,则“0<m<2”是三棱锥C﹣ABE的体积不小于1的( )
=m,则“0<m<2”是三棱锥C﹣ABE的体积不小于1的( ) 
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为菱形,PA⊥平面ABCD,E为PD的中点,F为AC和BD的交点.
(1)证明:PB∥平面AEC;
(2)证明:平面PAC⊥平面PBD.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直线AB经过⊙O上一点C,⊙O的半径为3,△AOB是等腰三角形,且C是AB中点,⊙O交直线OB于E、D. 
(1)证明:直线AB与⊙O相切;
(2)若∠CED的正切值为 ![]() ,求OA的长.
,求OA的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知空间中三点A(-2,0,2),B(-1,1,2),C(-3,0,4),设![]() =
=![]() ,
,![]() =
=![]() .
.
(1)求![]() 与
与![]() 的夹角的余弦值; (2)若
的夹角的余弦值; (2)若![]() 与k
与k![]() -2
-2![]() 互相垂直,求实数k的值.
互相垂直,求实数k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集U=R,集合A={x|7﹣6x≤0},集合B={x|y=lg(x+2)},则(UA)∩B等于( )
A.(﹣2, ![]() )
)
B.( ![]() ,+∞)
,+∞)
C.[﹣2, ![]() )
)
D.(﹣2,﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知等边![]() 中,
中,![]() 分别为
分别为![]() 边的中点,
边的中点,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 边上一点,且
边上一点,且![]() ,将
,将![]() 沿
沿![]() 折到
折到![]() 的位置,使平面
的位置,使平面![]() 平面EFCB.
平面EFCB.
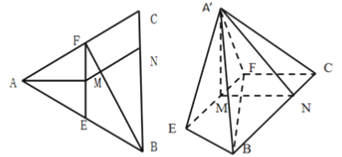
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD中,AB=1,BC=2,∠CBA= ![]() ,ABEF为直角梯形,BE∥AF,∠BAF=
,ABEF为直角梯形,BE∥AF,∠BAF= ![]() ,BE=2,AF=3,平面ABCD⊥平面ABEF.
,BE=2,AF=3,平面ABCD⊥平面ABEF. 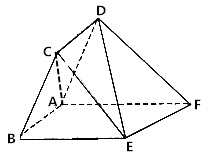
(1)求证:AC⊥平面ABEF;
(2)求平面ABCD与平面DEF所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
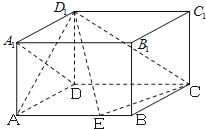
【题目】已知在长方体ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
(Ⅰ)求证:D1E⊥A1D;
(Ⅱ)在棱AB上是否存在点E使得AD1与平面D1EC成的角为![]() ?若存在,求出AE的长,若不存在,说明理由.
?若存在,求出AE的长,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com