
【题目】已知二次函数![]() 满足
满足![]() ,且
,且![]() .
.
![]() 求函数
求函数![]() 的解析式;
的解析式;
![]() 求
求![]() 在区间
在区间![]() 上的最大值和最小值;
上的最大值和最小值;
![]() 当
当![]() 时,
时,![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
【答案】(1)![]() ;(2)最大值为
;(2)最大值为![]() ,最小值为
,最小值为![]() ;(3)
;(3)![]() .
.
【解析】
![]() 根据题意,用待定系数法设二次函数的解析式为
根据题意,用待定系数法设二次函数的解析式为![]() ,由
,由![]() 得
得![]() ,又由
,又由![]() ,则
,则![]() ,即
,即![]() ,解可得a、b的值,代入函数的解析式,即可得答案;
,解可得a、b的值,代入函数的解析式,即可得答案;![]() 根据题意,由二次函数的性质分析可得答案;
根据题意,由二次函数的性质分析可得答案;![]() 根据题意,当
根据题意,当![]() 时,
时,![]() 恒成立,即
恒成立,即![]() 在
在![]() 上恒成立,由基本不等式的性质分析可得
上恒成立,由基本不等式的性质分析可得![]() ,则有
,则有![]() 在
在![]() 上恒成立,解可得a的取值范围,即可得答案.
上恒成立,解可得a的取值范围,即可得答案.
![]() 根据题意,设二次函数的解析式为
根据题意,设二次函数的解析式为![]()
由![]() 得
得![]() ,则
,则![]() ;
;
又由![]() ,则
,则![]() .
.
即![]() ,
,
则有![]() ,解可得
,解可得![]() ,
,![]() ,
,
故![]() ,
,
![]() 根据题意,由
根据题意,由![]() 的结论,
的结论,![]() ,
,
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,
上为增函数,
又由![]() ,
,![]() ,则
,则![]() ,
,
则![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() ;
;
![]() 根据题意,当
根据题意,当![]() 时,
时,![]() 恒成立,即
恒成立,即![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,
上恒成立,
又由分析可得:![]() ,则有
,则有![]() 在
在![]() 上恒成立,
上恒成立,
![]() ;
;
即a的取值范围为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+1|﹣2|x|.
(1)求不等式f(x)≤﹣6的解集;
(2)若存在实数x满足f(x)=log2a,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂有工人1000名,为了提高工人的生产技能,特组织工人参加培训.其中250名工人参加过短期培训(称为![]() 类工人),另外750名工人参加过长期培训(称为
类工人),另外750名工人参加过长期培训(称为![]() 类工人).现从该工厂的工人中共抽查了100名工人作为样本,调查他们的生产能力(生产能力是指工人一天加工的零件数),得到
类工人).现从该工厂的工人中共抽查了100名工人作为样本,调查他们的生产能力(生产能力是指工人一天加工的零件数),得到![]() 类工人生产能力的茎叶图(图1),
类工人生产能力的茎叶图(图1),![]() 类工人生产能力的频率分布直方图(图2).
类工人生产能力的频率分布直方图(图2).
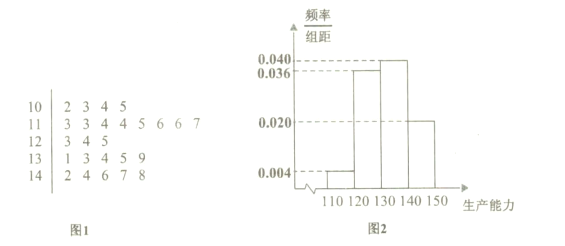
(1)在样本中求![]() 类工人生产能力的中位数,并估计
类工人生产能力的中位数,并估计![]() 类工人生产能力的平均数(同一组中的数据用该组区间的中点值作代表);
类工人生产能力的平均数(同一组中的数据用该组区间的中点值作代表);
(2)若规定生产能力在![]() 内为能力优秀,现以样本中频率作为概率,从1000名工人中按分层抽样共抽取
内为能力优秀,现以样本中频率作为概率,从1000名工人中按分层抽样共抽取![]() 名工人进行调查,请估计这
名工人进行调查,请估计这![]() 名工人中的各类人数,完成下面的
名工人中的各类人数,完成下面的![]() 列联表.
列联表.

若研究得到在犯错误的概率不超过![]() 的前提下,认为生产能力与培训时间长短有关,则
的前提下,认为生产能力与培训时间长短有关,则![]() 的最小值为多少?
的最小值为多少?
参考数据:

参考公式: 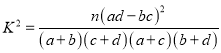 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x2+(a+1)x+a2(a∈R),若f(x)能表示成一个奇函数g(x)和一个偶函数h(x)的和.
(1)求g(x)和h(x)的解析式;
(2)若f(x)和g(x)在区间(-∞,(a+1)2]上都是减函数,求f(1)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() .
.
(1)求函数f(x)在[0,2]上得单调区间;
(2)当m=0,k∈R时,求函数g(x)=f(x)﹣kx2在R上零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2 sin(x+![]() )。
)。
(1)若点P(1,-![]() )在角
)在角![]() 的终边上,求:cos
的终边上,求:cos![]() 和f(
和f(![]() -
-![]() )的值;
)的值;
(2)若x![]() [
[![]() ,
, ![]() ],求f(x)的值域。
],求f(x)的值域。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足an+1+an=104n﹣1(n∈N*),数列{bn}的前n项和为Sn , 且bn=log2an .
(1)求bn , Sn;
(2)设cn= ![]() ,证明:
,证明: ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() Sn+1(n∈N*).
Sn+1(n∈N*).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com