
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源:2017届福建福州外国语学校高三适应性考试四数学(文)试卷(解析版) 题型:解答题
已知椭圆 经过点
经过点 ,离心率为
,离心率为 .
.
(1)求椭圆 的方程;
的方程;
(2)设直线 与椭圆
与椭圆 交于
交于 ,点
,点 关于
关于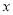 轴的对称点
轴的对称点 (
( 与
与 不重合),则直线
不重合),则直线 与
与 轴是否交于一定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由.
轴是否交于一定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2017届福建福州外国语学校高三适应性考试四数学(理)试卷(解析版) 题型:解答题
已知点 是直线
是直线 与椭圆
与椭圆 的一个公共点,
的一个公共点, 分别为该椭圆的左右焦点,设
分别为该椭圆的左右焦点,设 取得最小值时椭圆为
取得最小值时椭圆为 .
.
(I)求椭圆 的方程;
的方程;
(II)已知 是椭圆
是椭圆 上关于
上关于 轴对称的两点,
轴对称的两点,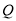 是椭圆
是椭圆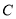 上异于
上异于 的任意一点,直线
的任意一点,直线 分别与
分别与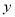 轴交于点
轴交于点 ,试判断
,试判断 是否为定值,并说明理由.
是否为定值,并说明理由.
查看答案和解析>>
科目:高中数学 来源:2017届福建福州外国语学校高三适应性考试四数学(理)试卷(解析版) 题型:选择题
一个几何体由多面体和旋转体的整体或一部分组合而成,其三视图如图所示,则该几何体的体积是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2017届山西大学附中高三二模测试数学试卷(解析版) 题型:选择题
双曲线 的左右焦点分别为
的左右焦点分别为 ,过
,过 的直线与双曲线的右支交于
的直线与双曲线的右支交于 两点,若
两点,若 是以
是以 为直角顶点的等腰直角三角形,则
为直角顶点的等腰直角三角形,则 ( )
( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2017届河南新乡市高三上学期第一次调研数学(理)试卷(解析版) 题型:解答题
甲、乙两位数学老师组队参加某电视台闯关节目,共3关,甲作为嘉宾参与答题,若甲回答错误,乙作为亲友团在整个通关过程中至多只能为甲提供一次帮助机会,若乙回答正确,则甲继续闯关,若某一关通不过,则收获前面所有累积奖金.约定每关通过得到奖金2000元,设甲每关通过的概率为 ,乙每关通过的概率为
,乙每关通过的概率为 ,且各关是否通过及甲、乙回答正确与否均相互独立.
,且各关是否通过及甲、乙回答正确与否均相互独立.
(1)求甲、乙获得2000元奖金的概率;
(2)设 表示甲、乙两人获得的奖金数,求随机变量
表示甲、乙两人获得的奖金数,求随机变量 的分布列和数学期望
的分布列和数学期望 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com