分析:(1)以D为坐标原点,以DA,DB,DC为x轴y轴z轴建立空间直角坐标系,利用
与的夹角余弦值求直线DB
1与BC
1夹角的余弦值.
(2)直线DB是直线B
1B在平面ABCD上的射影则AC⊥DB,根据三垂线定理,有AC⊥B
1B.过点A在平面ABB
1A
1内作AM⊥B
1B于M,连接MC,MO,由△AMB≌△CMB,得CM⊥BB
1,∠AMC是二面角A-B
1B-C的一个平面角,在三角形AMC中求出此角即可
解答:解:(1)以D为坐标原点,以DA,DB,DC为x轴y轴z轴建立空间直角坐标系.如图①
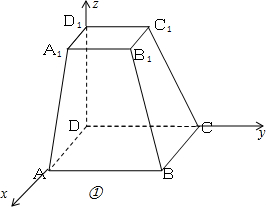
则各点坐标D(0,0,0),B(2,2,0),B
1(1,1,2),C
1(0,1,2)
=(1,1,2),
=(-2.-1,2)
设
,的夹角为θ,则cosθ=
=
=
直线DB
1与BC
1夹角的余弦值为
.
(2)如图②
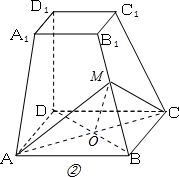
∵直线DB是直线B
1B在平面ABCD上的射影,AC⊥DB,
根据三垂线定理,有AC⊥B
1B.
过点A在平面ABB
1A
1内作AM⊥B
1B于M,连接MC,MO,
由△AMB≌△CMB,得CM⊥BB
1所以,∠AMC是二面角A-B
1B-C的一个平面角.
根据勾股定理,有
A1A=,C1C=,B1B=.
∵OM⊥B
1B,有
OM==,
BM=,
AM=,
CM=.
cos∠AMC==-.
点评:本小题主要考查直线与直线的夹角、二面角及其平面角等有关知识,考查空间想象能力和思维能力,属于中档题

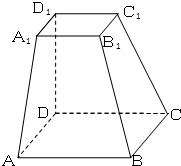 如图:在四棱台ABCD-A1B1C1D1中,DD1垂直底面,且DD1=2,底面四边形ABCD与A1B1C1D1分别为边长2和1的正方形.
如图:在四棱台ABCD-A1B1C1D1中,DD1垂直底面,且DD1=2,底面四边形ABCD与A1B1C1D1分别为边长2和1的正方形.



 备战中考寒假系列答案
备战中考寒假系列答案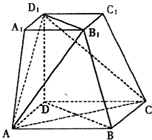 如图,在四棱台ABCD-A1B1C1D1中,下底ABCD是边长为2的正方形,上底A1B1C1D1是边长为1的正方形,侧棱DD1⊥平面ABCD,DD1=2.
如图,在四棱台ABCD-A1B1C1D1中,下底ABCD是边长为2的正方形,上底A1B1C1D1是边长为1的正方形,侧棱DD1⊥平面ABCD,DD1=2.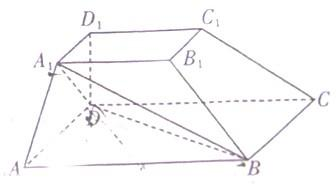
 (2009•聊城一模)如图,在四棱台ABCD-A1B1C1D1中,下底ABCD是边长为2的正方形,上底A1B1C1D1是边长为1的正方形,侧棱DD1⊥平面ABCD,DD1=2.
(2009•聊城一模)如图,在四棱台ABCD-A1B1C1D1中,下底ABCD是边长为2的正方形,上底A1B1C1D1是边长为1的正方形,侧棱DD1⊥平面ABCD,DD1=2.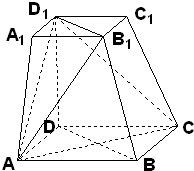 用平行于棱锥底面的平面去截棱锥,则截面与底面之间的部分叫棱台.如图,在四棱台ABCD-A1B1C1D1中,下底ABCD是边长为2的正方形,上底A1B1C1D1是边长为1的正方形,侧棱DD1⊥平面ABCD,DD1=2.
用平行于棱锥底面的平面去截棱锥,则截面与底面之间的部分叫棱台.如图,在四棱台ABCD-A1B1C1D1中,下底ABCD是边长为2的正方形,上底A1B1C1D1是边长为1的正方形,侧棱DD1⊥平面ABCD,DD1=2.