
°ĺŐ‚ńŅ°ŅÕ÷‘≤Ļś «Ľ≠Õ÷‘≤Ķń“Ľ÷÷Ļ§ĺŖ£¨»ÁÕľ1ňý ĺ£¨‘ŕ ģ◊÷–őĽ¨≤Ř…Ōłų”–“ĽłŲĽÓ∂ĮĽ¨ĪÍ![]() £¨
£¨![]() £¨”–“Ľłý–żłňĹęŃĹłŲĽ¨ĪÍѨ≥…“ĽŐŚ£¨
£¨”–“Ľłý–żłňĹęŃĹłŲĽ¨ĪÍѨ≥…“ĽŐŚ£¨![]() £¨
£¨![]() ő™–żłň…ŌĶń“ĽĶ„£¨«“‘ŕ
ő™–żłň…ŌĶń“ĽĶ„£¨«“‘ŕ![]() £¨
£¨![]() ŃĹĶ„÷ģľš£¨«“
ŃĹĶ„÷ģľš£¨«“![]() £¨ĶĪĽ¨ĪÍ
£¨ĶĪĽ¨ĪÍ![]() ‘༨≤Ř
‘༨≤Ř![]() ńŕ◊ųÕýłī‘ň∂Į£¨Ľ¨ĪÍ
ńŕ◊ųÕýłī‘ň∂Į£¨Ľ¨ĪÍ![]() ‘༨≤Ř
‘༨≤Ř![]() ńŕňś÷ģ‘ň∂Į Ī£¨ĹęĪ ľ‚∑Ň÷√”ŕ
ńŕňś÷ģ‘ň∂Į Ī£¨ĹęĪ ľ‚∑Ň÷√”ŕ![]() ī¶Ņ…Ľ≠≥ŲÕ÷‘≤£¨ľ«ł√Õ÷‘≤ő™
ī¶Ņ…Ľ≠≥ŲÕ÷‘≤£¨ľ«ł√Õ÷‘≤ő™![]() .»ÁÕľ2ňý ĺ£¨…Ť
.»ÁÕľ2ňý ĺ£¨…Ť![]() ”Ž
”Ž![]() ĹĽ”ŕĶ„
ĹĽ”ŕĶ„![]() £¨“‘
£¨“‘![]() ňý‘ŕĶń÷ĪŌŖő™
ňý‘ŕĶń÷ĪŌŖő™![]() ÷Š£¨“‘
÷Š£¨“‘![]() ňý‘ŕĶń÷ĪŌŖő™
ňý‘ŕĶń÷ĪŌŖő™![]() ÷Š£¨Ĺ®ŃĘ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ.
÷Š£¨Ĺ®ŃĘ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ.

£®1£©«ůÕ÷‘≤![]() Ķń∑Ĺ≥Ő£Ľ
Ķń∑Ĺ≥Ő£Ľ
£®2£©…Ť![]() £¨
£¨![]() «Õ÷‘≤
«Õ÷‘≤![]() Ķń◊ů”“∂•Ķ„£¨Ķ„
Ķń◊ů”“∂•Ķ„£¨Ķ„![]() ő™÷ĪŌŖ
ő™÷ĪŌŖ![]() …ŌĶń∂ĮĶ„£¨÷ĪŌŖ
…ŌĶń∂ĮĶ„£¨÷ĪŌŖ![]() £¨
£¨![]() ∑÷ĪūĹĽÕ÷‘≤”ŕ
∑÷ĪūĹĽÕ÷‘≤”ŕ![]() £¨
£¨![]() ŃĹĶ„£¨«ůňńĪŖ–ő
ŃĹĶ„£¨«ůňńĪŖ–ő![]() √śĽżő™
√śĽżő™![]() £¨«ůĶ„
£¨«ůĶ„![]() Ķń◊ÝĪÍ.
Ķń◊ÝĪÍ.
°ĺīūįł°Ņ£®1£©![]() £®2£©
£®2£©![]() ĽÚ
ĽÚ![]()
°ĺĹ‚őŲ°Ņ
£®1£©”…Ő‚Ķ√![]() £¨
£¨![]() £¨ĹŠļŌÕľ2£¨Ņ…÷™Õ÷‘≤
£¨ĹŠļŌÕľ2£¨Ņ…÷™Õ÷‘≤![]() Ķń≥§įŽ÷Š≥§ő™3£¨∂ŐįŽ÷Š≥§ő™1£¨Ļ Ņ…Ķ√Õ÷‘≤Ķń∑Ĺ≥Ő£Ľ
Ķń≥§įŽ÷Š≥§ő™3£¨∂ŐįŽ÷Š≥§ő™1£¨Ļ Ņ…Ķ√Õ÷‘≤Ķń∑Ĺ≥Ő£Ľ
£®2£©…ŤĶ„![]() £¨∆š÷–
£¨∆š÷–![]() £¨‘Ú÷ĪŌŖ
£¨‘Ú÷ĪŌŖ![]() Ķń∑Ĺ≥Őő™
Ķń∑Ĺ≥Őő™![]() £¨÷ĪŌŖ
£¨÷ĪŌŖ![]() Ķń∑Ĺ≥Őő™
Ķń∑Ĺ≥Őő™![]() £¨…Ť
£¨…Ť![]() £¨
£¨![]() £¨”…
£¨”… Ķ√
Ķ√![]() £¨ň„≥Ų
£¨ň„≥Ų![]() £¨Õ¨ņŪĶ√
£¨Õ¨ņŪĶ√![]() £¨ňý“‘Ķ√ňńĪŖ–ő
£¨ňý“‘Ķ√ňńĪŖ–ő![]() Ķń√śĽżő™
Ķń√śĽżő™ £¨ŃÓ
£¨ŃÓ![]() Ĺ‚∑Ĺ≥Ő«ů≥Ų
Ĺ‚∑Ĺ≥Ő«ů≥Ų![]() £¨ĶĪ
£¨ĶĪ![]() Ī£¨”…∂‘≥∆–‘Ņ…Ķ√
Ī£¨”…∂‘≥∆–‘Ņ…Ķ√![]() £¨Ļ Ņ…Ķ√∑ŻļŌŐűľĢĶńĶ„
£¨Ļ Ņ…Ķ√∑ŻļŌŐűľĢĶńĶ„![]() .
.
£®1£©”…Ő‚Ķ√![]() £¨
£¨![]() £¨ňý“‘Õ÷‘≤
£¨ňý“‘Õ÷‘≤![]() Ķń≥§įŽ÷Š≥§ő™3£¨∂ŐįŽ÷Š≥§ő™1£¨
Ķń≥§įŽ÷Š≥§ő™3£¨∂ŐįŽ÷Š≥§ő™1£¨
Ļ Õ÷‘≤![]() Ķń∑Ĺ≥Őő™£ļ
Ķń∑Ĺ≥Őő™£ļ![]() £Ľ
£Ľ
£®2£©…ŤĶ„![]() £¨∆š÷–
£¨∆š÷–![]() £¨‘Ú÷ĪŌŖ
£¨‘Ú÷ĪŌŖ![]() Ķń∑Ĺ≥Őő™
Ķń∑Ĺ≥Őő™![]() £¨÷ĪŌŖ
£¨÷ĪŌŖ![]() Ķń∑Ĺ≥Őő™
Ķń∑Ĺ≥Őő™![]() .…Ť
.…Ť![]() £¨
£¨![]() .
.
”… £¨ŌŻ
£¨ŌŻ![]() Ķ√
Ķ√![]() £¨”…”ŕ
£¨”…”ŕ![]() £¨‘Ú
£¨‘Ú![]() .
.
”… £¨ŌŻ
£¨ŌŻ![]() Ķ√
Ķ√![]() £¨”…”ŕ
£¨”…”ŕ![]() £¨‘Ú
£¨‘Ú![]() .
.
ňý“‘ňńĪŖ–ő![]() Ķń√śĽżő™
Ķń√śĽżő™
 .
.
”…”ŕ![]() £¨
£¨![]() £¨
£¨
Ļ  .
.
Ĺ‚Ķ√![]() ĽÚ
ĽÚ![]() £®…Š»•£©£¨ľī
£®…Š»•£©£¨ľī![]() £¨ĶĪ
£¨ĶĪ![]() Ī£¨”…∂‘≥∆–‘Ņ…Ķ√
Ī£¨”…∂‘≥∆–‘Ņ…Ķ√![]() £¨.
£¨.
◊Ř…Ō£¨ĶĪĶ„![]() ĽÚ
ĽÚ![]() Ī£¨ňńĪŖ–ő
Ī£¨ňńĪŖ–ő![]() Ķń√śĽżő™
Ķń√śĽżő™![]() .
.



| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°ŅĻŕ◊ī≤°∂ĺ «“ĽłŲīů–Õ≤°∂ĺľ“◊Ś£¨ľļ÷™Ņ…“ż∆ūł–√į“‘ľį÷–∂ęļŰőŁ◊ŘļŌ’ų£®![]() £©ļÕ—Ō÷ōľĪ–‘ļŰőŁ◊ŘļŌ’ų£®
£©ļÕ—Ō÷ōľĪ–‘ļŰőŁ◊ŘļŌ’ų£®![]() £©Ķ»ĹŌ—Ō÷ōľ≤≤°.∂ÝĹŮńÍ≥ŲŌ÷‘ŕļĢĪĪőšļļĶń–¬–ÕĻŕ◊ī≤°∂ĺ£®
£©Ķ»ĹŌ—Ō÷ōľ≤≤°.∂ÝĹŮńÍ≥ŲŌ÷‘ŕļĢĪĪőšļļĶń–¬–ÕĻŕ◊ī≤°∂ĺ£®![]() £© «“‘«įī”őī‘ŕ»ňŐŚ÷–∑ĘŌ÷ĶńĻŕ◊ī≤°∂ĺ–¬∂ĺ÷Í.»ňł–»ĺŃň–¬–ÕĻŕ◊ī≤°∂ĺļů≥£ľŻŐŚ’ų”–ļŰőŁĶņ÷Ę◊ī°Ę∑Ę»»°ĘŅ»ň‘°Ę∆ÝīŔļÕļŰőŁņßń—Ķ».‘ŕĹŌ—Ō÷ō≤°ņż÷–£¨ł–»ĺŅ…Ķľ÷¬∑ő—◊°Ę—Ō÷ōľĪ–‘ļŰőŁ◊ŘļŌ’ų°Ę…Ųň•ĹŖ£¨…ű÷ŃňņÕŲ.
£© «“‘«įī”őī‘ŕ»ňŐŚ÷–∑ĘŌ÷ĶńĻŕ◊ī≤°∂ĺ–¬∂ĺ÷Í.»ňł–»ĺŃň–¬–ÕĻŕ◊ī≤°∂ĺļů≥£ľŻŐŚ’ų”–ļŰőŁĶņ÷Ę◊ī°Ę∑Ę»»°ĘŅ»ň‘°Ę∆ÝīŔļÕļŰőŁņßń—Ķ».‘ŕĹŌ—Ō÷ō≤°ņż÷–£¨ł–»ĺŅ…Ķľ÷¬∑ő—◊°Ę—Ō÷ōľĪ–‘ļŰőŁ◊ŘļŌ’ų°Ę…Ųň•ĹŖ£¨…ű÷ŃňņÕŲ.
ń≥“Ĺ‘ļő™…ł≤ťĻŕ◊ī≤°∂ĺ£¨–Ť“™ľž—ť—™“ļ «∑Ůő™—Ű–‘£¨Ō÷”–n£®![]() £©∑›—™“ļ—ýĪĺ£¨”–“‘Ō¬ŃĹ÷÷ľž—ť∑Ĺ Ĺ£ļ
£©∑›—™“ļ—ýĪĺ£¨”–“‘Ō¬ŃĹ÷÷ľž—ť∑Ĺ Ĺ£ļ
∑Ĺ Ĺ“Ľ£ļ÷ū∑›ľž—ť£¨‘Ú–Ť“™ľž—ťnīő.
∑Ĺ Ĺ∂Ģ£ļĽžļŌľž—ť£¨Ĺę∆š÷–k£®![]() «“
«“![]() £©∑›—™“ļ—ýĪĺ∑÷Īū»°—ýĽžļŌ‘ŕ“Ľ∆ūľž—ť.
£©∑›—™“ļ—ýĪĺ∑÷Īū»°—ýĽžļŌ‘ŕ“Ľ∆ūľž—ť.
»Űľž—ťĹŠĻŻő™“ű–‘£¨’‚k∑›Ķń—™“ļ»ęő™“ű–‘£¨“Ú∂Ý’‚k∑›—™“ļ—ýĪĺ÷Ľ“™ľž—ť“ĽīőĺÕĻĽŃň£¨»ÁĻŻľž—ťĹŠĻŻő™—Ű–‘£¨ő™Ńň√ų»∑’‚k∑›—™“ļĺŅĺĻńńľł∑›ő™—Ű–‘£¨ĺÕ“™∂‘’‚k∑›‘Ŕ÷ū∑›ľž—ť£¨īň Ī’‚k∑›—™“ļĶńľž—ťīő ż◊‹Ļ≤ő™![]() .
.
ľŔ…Ť‘ŕĹ” ‹ľž—ťĶń—™“ļ—ýĪĺ÷–£¨√Ņ∑›—ýĪĺĶńľž—ťĹŠĻŻ «—Ű–‘ĽĻ «“ű–‘∂ľ «∂ņŃĘĶń£¨«“√Ņ∑›—ýĪĺ «—Ű–‘ĹŠĻŻĶńłŇ¬ ő™p£®![]() £©.Ō÷»°∆š÷–k£®
£©.Ō÷»°∆š÷–k£®![]() «“
«“![]() £©∑›—™“ļ—ýĪĺ£¨ľ«≤…”√÷ū∑›ľž—ť∑Ĺ Ĺ£¨—ýĪĺ–Ť“™ľž—ťĶń◊‹īő żő™
£©∑›—™“ļ—ýĪĺ£¨ľ«≤…”√÷ū∑›ľž—ť∑Ĺ Ĺ£¨—ýĪĺ–Ť“™ľž—ťĶń◊‹īő żő™![]() £¨≤…”√ĽžļŌľž—ť∑Ĺ Ĺ£¨—ýĪĺ–Ť“™ľž—ťĶń◊‹īő żő™
£¨≤…”√ĽžļŌľž—ť∑Ĺ Ĺ£¨—ýĪĺ–Ť“™ľž—ťĶń◊‹īő żő™![]() .
.
£®1£©»Ű![]() £¨ ‘«ůpĻō”ŕkĶńļĮ żĻōŌĶ Ĺ
£¨ ‘«ůpĻō”ŕkĶńļĮ żĻōŌĶ Ĺ![]() £Ľ
£Ľ
£®2£©»Űp”Žł…»Ňňōľ∆ŃŅ![]() ŌŗĻō£¨∆š÷–
ŌŗĻō£¨∆š÷–![]() £®
£®![]() £© «≤ĽÕ¨Ķń’ż Ķ ż£¨
£© «≤ĽÕ¨Ķń’ż Ķ ż£¨
¬ķ◊„![]() «“
«“![]() £®
£®![]() £©∂ľ”–
£©∂ľ”–![]() ≥…ŃĘ.
≥…ŃĘ.
£®i£©«ů÷§£ļ żŃ–![]() Ķ»Ī» żŃ–£Ľ
Ķ»Ī» żŃ–£Ľ
£®ii£©ĶĪ![]() Ī£¨≤…”√ĽžļŌľž—ť∑Ĺ ĹŅ…“‘ ĻĶ√—ýĪĺ–Ť“™ľž—ťĶń◊‹īő żĶń∆ŕÕŻ÷ĶĪ»÷ū∑›ľž—ťĶń◊‹īő żĶń∆ŕÕŻ÷ĶłŁ…Ŕ£¨«ůkĶń◊Óīů÷Ķ
Ī£¨≤…”√ĽžļŌľž—ť∑Ĺ ĹŅ…“‘ ĻĶ√—ýĪĺ–Ť“™ľž—ťĶń◊‹īő żĶń∆ŕÕŻ÷ĶĪ»÷ū∑›ľž—ťĶń◊‹īő żĶń∆ŕÕŻ÷ĶłŁ…Ŕ£¨«ůkĶń◊Óīů÷Ķ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™Õ÷‘≤![]() £ļ
£ļ![]() ĶńņŽ–ń¬ ő™
ĶńņŽ–ń¬ ő™![]() £¨«“ĺ≠ĻżĶ„
£¨«“ĺ≠ĻżĶ„![]() .
.
£®1£©«ůÕ÷‘≤![]() Ķń∑Ĺ≥Ő£Ľ
Ķń∑Ĺ≥Ő£Ľ
£®2£©ĻżĶ„![]() ◊ų÷ĪŌŖĹĽÕ÷‘≤
◊ų÷ĪŌŖĹĽÕ÷‘≤![]() ”ŕ
”ŕ![]() £¨
£¨![]() ŃĹĶ„£¨»ŰĶ„
ŃĹĶ„£¨»ŰĶ„![]() Ļō”ŕ
Ļō”ŕ![]() ÷ŠĶń∂‘≥∆Ķ„ő™
÷ŠĶń∂‘≥∆Ķ„ő™![]() £¨÷§√ų÷ĪŌŖ
£¨÷§√ų÷ĪŌŖ![]() Ļż∂®Ķ„.
Ļż∂®Ķ„.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ‘ŕňńņ‚◊∂![]() ÷–£¨
÷–£¨![]() ∆Ĺ√ś
∆Ĺ√ś![]() £¨
£¨![]() £¨Ķ„
£¨Ķ„![]() «ĺō–ő
«ĺō–ő![]() ńŕ£®ļ¨ĪŖĹÁ£©Ķń∂ĮĶ„£¨«“
ńŕ£®ļ¨ĪŖĹÁ£©Ķń∂ĮĶ„£¨«“![]() £¨
£¨![]() £¨÷ĪŌŖ
£¨÷ĪŌŖ![]() ”Ž∆Ĺ√ś
”Ž∆Ĺ√ś![]() ňý≥…ĶńĹ«ő™
ňý≥…ĶńĹ«ő™![]() .ľ«Ķ„
.ľ«Ķ„![]() ĶńĻžľ£≥§∂»ő™
ĶńĻžľ£≥§∂»ő™![]() £¨‘Ú
£¨‘Ú![]() ______£ĽĶĪ»żņ‚◊∂
______£ĽĶĪ»żņ‚◊∂![]() ĶńŐŚĽż◊Ó–° Ī£¨»żņ‚◊∂
ĶńŐŚĽż◊Ó–° Ī£¨»żņ‚◊∂![]() ĶńÕ‚Ĺ”«ÚĶńĪŪ√śĽżő™______.
ĶńÕ‚Ĺ”«ÚĶńĪŪ√śĽżő™______.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨ňńņ‚◊∂P©ĀABCDĶńĶ◊√śABCD «’ż∑Ĺ–ő£¨PA°ÕĶ◊√śABCD£¨E£¨F∑÷Īū «AC£¨PBĶń÷–Ķ„£ģ
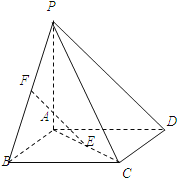
£®1£©÷§√ų£ļEF°ő∆Ĺ√śPCD£Ľ
£®2£©«ů÷§£ļ√śPBD°Õ√śPAC£Ľ
£®3£©»ŰPA=AB£¨«ůPD”Ž∆Ĺ√śPACňý≥…Ĺ«Ķńīů–°£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™ļĮ ż![]()
![]() .
.
£®1£©÷§√ų£ļĶĪ![]() Ī£¨
Ī£¨![]() ”–◊Ó–°÷Ķ£¨őř◊Óīů÷Ķ£Ľ
”–◊Ó–°÷Ķ£¨őř◊Óīů÷Ķ£Ľ
£®2£©»Ű‘ŕ«Ýľš![]() …Ō∑Ĺ≥Ő
…Ō∑Ĺ≥Ő![]() «°”–“ĽłŲ Ķ żłý£¨«ů
«°”–“ĽłŲ Ķ żłý£¨«ů![]() Ķń»°÷Ķ∑∂őß.
Ķń»°÷Ķ∑∂őß.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ‘ŕ÷ĪĹ«◊ÝĪÍŌĶ![]() ÷–£¨“—÷™Ķ„
÷–£¨“—÷™Ķ„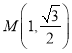 £¨
£¨![]() Ķń≤ő ż∑Ĺ≥Őő™
Ķń≤ő ż∑Ĺ≥Őő™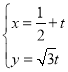 £®
£®![]() ő™≤ő ż£©£¨“‘◊ÝĪÍ‘≠Ķ„
ő™≤ő ż£©£¨“‘◊ÝĪÍ‘≠Ķ„![]() ő™ľęĶ„£¨
ő™ľęĶ„£¨![]() ÷ŠĶń’żįŽ÷Šő™ľę÷Š£¨Ĺ®ŃĘľę◊ÝĪÍŌĶ£¨«ķŌŖ
÷ŠĶń’żįŽ÷Šő™ľę÷Š£¨Ĺ®ŃĘľę◊ÝĪÍŌĶ£¨«ķŌŖ![]() Ķńľę◊ÝĪÍ∑Ĺ≥Őő™
Ķńľę◊ÝĪÍ∑Ĺ≥Őő™![]() .
.
£®1£©«ů![]() Ķń∆’Õ®∑Ĺ≥ŐļÕ
Ķń∆’Õ®∑Ĺ≥ŐļÕ![]() Ķń÷ĪĹ«◊ÝĪÍ∑Ĺ≥Ő£Ľ
Ķń÷ĪĹ«◊ÝĪÍ∑Ĺ≥Ő£Ľ
£®2£©…Ť«ķŌŖ![]() ”Ž«ķŌŖ
”Ž«ķŌŖ![]() ŌŗĹĽ”ŕ
ŌŗĹĽ”ŕ![]() £¨
£¨![]() ŃĹĶ„£¨«ů
ŃĹĶ„£¨«ů![]() Ķń÷Ķ.
Ķń÷Ķ.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņń≥≤ÕŐŁÕ®Ļż≤ť‘ńŃň◊ÓĹŁ5īő ≥∆∑ĹĽ“◊ĽŠ≤őĽŠ»ň ż![]() (ÕÚ»ň)”Ž≤ÕŐŁňý”√‘≠≤ńŃŌ żŃŅ
(ÕÚ»ň)”Ž≤ÕŐŁňý”√‘≠≤ńŃŌ żŃŅ![]() (īŁ)£¨Ķ√ĶĹ»ÁŌ¬Õ≥ľ∆ĪŪ£ļ
(īŁ)£¨Ķ√ĶĹ»ÁŌ¬Õ≥ľ∆ĪŪ£ļ
Ķŕ“Ľīő | Ķŕ∂Ģīő | Ķ໿īő | Ķŕňńīő | ĶŕőŚīő | |
≤őĽŠ»ň ż | 13 | 9 | 8 | 10 | 12 |
‘≠≤ńŃŌ | 32 | 23 | 18 | 24 | 28 |
£®1£©łýĺ›ňýłÝ5◊ť żĺ›£¨«ů≥Ų![]() Ļō”ŕ
Ļō”ŕ![]() ĶńŌŖ–‘ĽōĻť∑Ĺ≥Ő
ĶńŌŖ–‘ĽōĻť∑Ĺ≥Ő![]() .
.
£®2£©“—÷™Ļļ¬Ú‘≠≤ńŃŌĶń∑—”√![]() (‘™)”Ž żŃŅ
(‘™)”Ž żŃŅ![]() (īŁ)ĶńĻōŌĶő™
(īŁ)ĶńĻōŌĶő™![]() £¨
£¨
Õ∂»Ž Ļ”√Ķń√ŅīŁ‘≠≤ńŃŌŌŗ”¶ĶńŌķ Ř ’»Žő™700‘™£¨∂ŗ”ŗĶń‘≠≤ńŃŌ÷Ľń‹őř≥•∑ĶĽĻ£¨ĺ›Ō§ĪĺīőĹĽ“◊īůĽŠīů‘ľ”–15ÕÚ»ň≤őľ”£¨łýĺ›(1)÷–«ů≥ŲĶńŌŖ–‘ĽōĻť∑Ĺ≥Ő£¨‘§≤‚≤ÕŐŁ”¶Ļļ¬Ú∂ŗ…ŔīŁ‘≠≤ńŃŌ£¨≤Ňń‹ĽŮĶ√◊ÓīůņŻ»ů£¨◊ÓīůņŻ»ů «∂ŗ…Ŕ£Ņ(◊Ę£ļņŻ»ů![]() Ōķ Ř ’»Ž
Ōķ Ř ’»Ž![]() ‘≠≤ńŃŌ∑—”√).
‘≠≤ńŃŌ∑—”√).
≤őŅľĻę Ĺ£ļ  £¨
£¨ ![]() .
.
≤őŅľ żĺ›£ļ ![]() £¨
£¨ ![]() £¨
£¨ ![]() .
.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕňńņ‚◊∂![]() ÷–£¨Ķ◊√ś
÷–£¨Ķ◊√ś![]() «ĺō–ő£¨≤ŗņ‚
«ĺō–ő£¨≤ŗņ‚![]() Ķ◊√ś
Ķ◊√ś![]() £¨
£¨![]() £¨Ķ„
£¨Ķ„![]() «
«![]() Ķń÷–Ķ„.
Ķń÷–Ķ„.
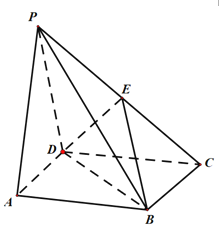
![]() «ů÷§£ļ
«ů÷§£ļ![]() ∆Ĺ√ś
∆Ĺ√ś![]() £Ľ
£Ľ
![]() »Ű÷ĪŌŖ
»Ű÷ĪŌŖ![]() ”Ž∆Ĺ√ś
”Ž∆Ĺ√ś![]() ňý≥…Ĺ«ő™
ňý≥…Ĺ«ő™![]() £¨«ů∂Ģ√śĹ«
£¨«ů∂Ģ√śĹ«![]() Ķńīů–°.
Ķńīů–°.
≤ťŅīīūįłļÕĹ‚őŲ>>
įŔ∂»÷¬–Ň - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com