
【题目】如图,在多面体ABCDEF中,四边形ABCD是菱形,AC,BD相交于点O,EF∥AB,AB=2EF,平面BCF⊥平面ABCD,BF=CF,点G为BC的中点.求证:
(1) 直线OG∥平面EFCD;
(2) 直线AC⊥平面ODE.

【答案】证明:(1) 见解析: (2) 见解析.
【解析】试题分析:
(1)利用题意证得OG∥CD,结合线面平行的判断定理即可证得结论;
(2)结合空间几何体的性质和线面垂直的判断定理即可证得题中的结论.
试题解析:
证明:(1) ∵ 四边形ABCD是菱形,AC∩BD=O,
∴ 点O是BD的中点.
∵ 点G为BC的中点,∴ OG∥CD.
∵ OG平面EFCD,CD平面EFCD,
∴ 直线OG∥平面EFCD.
(2) ∵ BF=CF,点G为BC的中点,
∴ FG⊥BC.
∵ 平面BCF⊥平面ABCD,平面BCF∩平面ABCD=BC,FG平面BCF,FG⊥BC,
∴ FG⊥平面ABCD.
∵ AC平面ABCD,∴ FG⊥AC.
∵ OG∥AB,OG=AB,EF∥AB,EF=AB,
∴ OG∥EF,OG=EF,
∴ 四边形EFGO为平行四边形,
∴ FG∥EO.
∴ AC⊥EO.
∵ 四边形ABCD是菱形,∴ AC⊥DO.
∵ EO∩DO=O,EO,DO在平面ODE内,
∴ AC⊥平面ODE.


科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若![]() 的值域为
的值域为![]() ,求
,求![]() 的值;
的值;
(Ⅱ)巳![]() ,是否存在这祥的实数
,是否存在这祥的实数![]() ,使函数
,使函数![]() 在区间
在区间![]() 内有且只有一个零点.若存在,求出
内有且只有一个零点.若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,其前
,其前![]() 项和为
项和为![]() ,满足
,满足![]() ,
,![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,
,![]() .
.
⑴若![]() ,
,![]() ,
,![]() (
(![]() ),求证:数列
),求证:数列![]() 是等比数列;
是等比数列;
⑵若数列![]() 是等比数列,求
是等比数列,求![]() ,
,![]() 的值;
的值;
⑶若![]() ,且
,且![]() ,求证:数列
,求证:数列![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了检验学习情况,某培训机构于近期举办一场竞赛活动,分别从甲、乙两班各抽取10名学员的成绩进行统计分析,其成绩的茎叶图如图所示(单位:分),假设成绩不低于90分者命名为“优秀学员”.
(1)分别求甲、乙两班学员成绩的平均分(结果保留一位小数);
(2)从甲班4名优秀学员中抽取两人,从乙班2名80分以下的学员中抽取一人,求三人平均分不低于90分的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.
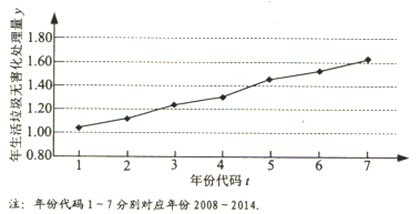
(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据:![]() ,
,![]() ,
,
![]() ,
,![]() ≈2.646.
≈2.646.
参考公式:相关系数
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】衡阳市八中对参加“社会实践活动”的全体志愿者进行学分考核,因该批志愿者表现良好,学校决定考核只有合格和优秀两个等次.若某志愿者考核为合格,授予1个学分;考核为优秀,授予2个学分,假设该校志愿者甲、乙、丙考核为优秀的概率分别为![]() 、
、![]() 、
、![]() ,他们考核所得的等次相互独立.
,他们考核所得的等次相互独立.
(1)求在这次考核中,志愿者甲、乙、丙三人中至少有一名考核为优秀的概率;
(2)记在这次考核中甲、乙、丙三名志愿者所得学分之和为随机变量![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
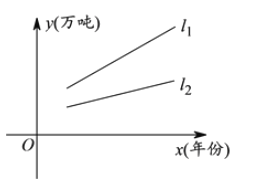
【题目】对某种产品市场产销量情况如图所示,其中:![]() 表示产品各年年产量的变化规律;
表示产品各年年产量的变化规律;![]() 表示产品各年的销售情况.下列叙述:(1)产品产量、销售量均以直线上升,仍可按原生产计划进行下去;(2)产品已经出现了供大于求的情况,价格将趋跌;(3)产品的库存积压将越来越严重,应压缩产量或扩大销售量;(4)产品的产、销情况均以一定的年增长率递增.你认为较合理的是( )
表示产品各年的销售情况.下列叙述:(1)产品产量、销售量均以直线上升,仍可按原生产计划进行下去;(2)产品已经出现了供大于求的情况,价格将趋跌;(3)产品的库存积压将越来越严重,应压缩产量或扩大销售量;(4)产品的产、销情况均以一定的年增长率递增.你认为较合理的是( )
A.(1),(2),(3)B.(1),(3),(4)
C.(2),(4)D.(2),(3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com