
【题目】把边长为6的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为![]() ,容积为
,容积为![]() .
.
(1)写出函数![]() 的解析式,并求出函数的定义域;
的解析式,并求出函数的定义域;
(2)求当![]() 为多少时,容器的容积最大?并求出最大容积.
为多少时,容器的容积最大?并求出最大容积.
【答案】(Ⅰ)![]() ,定义域为
,定义域为![]() .(Ⅱ)容器高为
.(Ⅱ)容器高为![]() 时,容器的容积最大为
时,容器的容积最大为![]() .
.
【解析】
试题(Ⅰ)根据容器的高为x,求得做成的正三棱柱形容器的底边长,从而可得函数V(x)的解析式,函数的定义域;(Ⅱ)实际问题归结为求函数V(x)在区间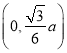 上的最大值点,先求V(x)的极值点,再确定极大值就是最大值即可
上的最大值点,先求V(x)的极值点,再确定极大值就是最大值即可
试题解析:(Ⅰ)因为容器的高为x,则做成的正三棱柱形容器的底边长为![]()
则![]() .
.
函数的定义域为![]() .
.
(Ⅱ)实际问题归结为求函数![]() 在区间
在区间![]() 上的最大值点.
上的最大值点.
先求![]() 的极值点.
的极值点.
在开区间![]() 内,
内,![]()
令![]() ,即令
,即令![]() ,解得
,解得![]() .
.
因为![]() 在区间
在区间![]() 内,
内,![]() 可能是极值点. 当
可能是极值点. 当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
因此![]() 是极大值点,且在区间
是极大值点,且在区间![]() 内,
内,![]() 是唯一的极值点,
是唯一的极值点,
所以![]() 是
是![]() 的最大值点,并且最大值
的最大值点,并且最大值![]()
即当正三棱柱形容器高为![]() 时,容器的容积最大为
时,容器的容积最大为![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】从1到9的九个数字中取三个偶数四个奇数,试问:
①能组成多少个没有重复数字的七位数?
②上述七位数中三个偶数排在一起的有几个?
③在①中的七位数中,偶数排在一起、奇数也排在一起的有几个?
④在①中任意两偶数都不相邻的七位数有几个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将![]() 颗珠子分成
颗珠子分成![]() 堆.若通过每次从其中
堆.若通过每次从其中![]() 堆中各取走一颗珠子,而最后取完,则称这样的分法为“和谐的”.试给出和谐分法的充分必要条件,并加以证明.
堆中各取走一颗珠子,而最后取完,则称这样的分法为“和谐的”.试给出和谐分法的充分必要条件,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司招聘员工,先由两位专家面试,若两位专家都同意通过,则视作通过初审予以录用;若这两位专家都未同意通过,则视作未通过初审不予录用;当这两位专家意见不一致时,再由第三位专家进行复审,若能通过复审则予以录用,否则不予录用.设应聘人员获得每位初审专家通过的概率均为![]() ,复审能通过的概率为
,复审能通过的概率为![]() ,各专家评审的结果相互独立.
,各专家评审的结果相互独立.
(1)求某应聘人员被录用的概率;
(2)若4人应聘,设X为被录用的人数,试求随机变量X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]()

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系xOy中,曲线C1的普通方程为![]() ,曲线C2参数方程为
,曲线C2参数方程为![]() 为参数),以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,直线l的极坐标方程为
为参数),以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,直线l的极坐标方程为![]() .
.
(1)求C1的参数方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)已知P是C2上参数![]() 对应的点,Q为C1上的点,求PQ中点M到直线
对应的点,Q为C1上的点,求PQ中点M到直线![]() 的距离取得最大值时,点Q的直角坐标.
的距离取得最大值时,点Q的直角坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com