
【题目】为吸引顾客,某公司在商场举办电子游戏活动.对于![]() 两种游戏,每种游戏玩一次均会出现两种结果,而且每次游戏的结果相互独立,具体规则如下:玩一次游戏
两种游戏,每种游戏玩一次均会出现两种结果,而且每次游戏的结果相互独立,具体规则如下:玩一次游戏![]() ,若绿灯闪亮,获得
,若绿灯闪亮,获得![]() 分,若绿灯不闪亮,则扣除
分,若绿灯不闪亮,则扣除![]() 分(即获得
分(即获得![]() 分),绿灯闪亮的概率为
分),绿灯闪亮的概率为![]() ;玩一次游戏
;玩一次游戏![]() ,若出现音乐,获得
,若出现音乐,获得![]() 分,若没有出现音乐,则扣除
分,若没有出现音乐,则扣除![]() 分(即获得
分(即获得![]() 分),出现音乐的概率为
分),出现音乐的概率为![]() .玩多次游戏后累计积分达到
.玩多次游戏后累计积分达到![]() 分可以兑换奖品.
分可以兑换奖品.
(1)记![]() 为玩游戏
为玩游戏![]() 和
和![]() 各一次所得的总分,求随机变量
各一次所得的总分,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(2)记某人玩![]() 次游戏
次游戏![]() ,求该人能兑换奖品的概率.
,求该人能兑换奖品的概率.
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1)随机变量![]() 可取的数值为
可取的数值为![]() ,每一种情况为两种游戏的结果的概率的乘积,求出概率再求分布列和期望;(2)每次得60分的概率为
,每一种情况为两种游戏的结果的概率的乘积,求出概率再求分布列和期望;(2)每次得60分的概率为![]() ,扣20分的概率为
,扣20分的概率为![]() ,设需出现
,设需出现![]() 次音乐,那么
次音乐,那么![]() ,计算
,计算![]() 值,再求其概率.
值,再求其概率.
试题解析:(1)随机变量![]() 的所有可能取值为
的所有可能取值为![]() ,分别对应以下四种情况:
,分别对应以下四种情况:
①玩游戏![]() ,绿灯闪亮,且玩游戏
,绿灯闪亮,且玩游戏![]() ,出现音乐;
,出现音乐;
②玩游戏![]() ,绿灯不闪亮,且玩游戏
,绿灯不闪亮,且玩游戏![]() ,出现音乐;
,出现音乐;
③玩游戏![]() ,绿灯闪亮,且玩游戏
,绿灯闪亮,且玩游戏![]() ,没有出现音乐;
,没有出现音乐;
④玩游戏![]() ,绿灯不闪亮,且玩游戏
,绿灯不闪亮,且玩游戏![]() ,没有出现音乐,
,没有出现音乐,
所以![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
即![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
|
|
![]() .
.
(2)设某人玩![]() 次游戏
次游戏![]() 的过程中,出现音乐
的过程中,出现音乐![]() 次,则没出现音乐
次,则没出现音乐![]() 次,依题意得
次,依题意得![]() ,解得
,解得![]() ,所以
,所以![]() 或
或![]() 或
或![]() .
.
设“某人玩![]() 次游戏
次游戏![]() 能兑换奖品”为事件
能兑换奖品”为事件![]() ,
,
则![]() .
.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的长轴是短轴的两倍,点P(
=1(a>b>0)的长轴是短轴的两倍,点P( ![]() ,
, ![]() )在椭圆上,不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为k1、k、k2 , 且k1、k、k2恰好构成等比数列,记△AOB的面积为S.
)在椭圆上,不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为k1、k、k2 , 且k1、k、k2恰好构成等比数列,记△AOB的面积为S. 
(1)求椭圆C的方程;
(2)试判断|OA|2+|OB|2是否为定值?若是,求出这个值;若不是,请说明理由?
(3)求△AOB面积S的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=x2+2(a﹣1)x+2在区间[﹣1,2]上单调,则实数a的取值范围为( )
A.[2,+∞)
B.(﹣∞,﹣1]
C.(﹣∞,﹣1]∪[2,+∞)
D.(﹣∞,﹣1)∪(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校![]() 届高三文(1)班在一次数学测验中,全班
届高三文(1)班在一次数学测验中,全班![]() 名学生的数学成绩的频率分布直方图如下,已知分数在
名学生的数学成绩的频率分布直方图如下,已知分数在![]() 的学生数有
的学生数有![]() 人.
人.
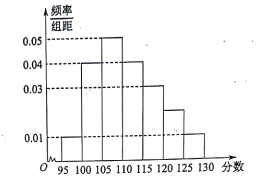
(1)求总人数![]() 和分数在
和分数在![]() 的人数
的人数![]() ;
;
(2)利用频率分布直方图,估算该班学生数学成绩的众数和中位数各是多少?
(3)现在从比分数在![]() 名学生(男女生比例为
名学生(男女生比例为![]() )中任选
)中任选![]() 人,求其中至多含有
人,求其中至多含有![]() 名男生的概率.
名男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .直线
.直线![]() 交曲线
交曲线![]() 于
于![]() 两点.
两点.
(1)写出直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的直角坐标为
的直角坐标为![]() ,求点
,求点![]() 到
到![]() 两点的距离之积.
两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y= ![]() +lg(﹣x2+4x﹣3)的定义域为M,
+lg(﹣x2+4x﹣3)的定义域为M,
(1)求M;
(2)当x∈M时,求函数f(x)=a2x+2+34x(a<﹣3)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B、C是椭圆M: ![]() =1(a>b>0)上的三点,其中点A的坐标为
=1(a>b>0)上的三点,其中点A的坐标为 ![]() ,BC过椭圆M的中心,且
,BC过椭圆M的中心,且 ![]() .
.
(1)求椭圆M的方程;
(2)过点(0,t)的直线l(斜率存在时)与椭圆M交于两点P、Q,设D为椭圆M与y轴负半轴的交点,且 ![]() ,求实数t的取值范围.
,求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com