
分析 利用待定系数法将直线x=b函数取得最小值为3,且经过点M(2,4代入二次函数解析式,求二次函数解析式即可.
解答 解:函数的对称轴为x=b,开口向上,
二次函数f(x)=x2-2bx+c的最小值为3,它的图象过点M(2,4),
可得:$\left\{\begin{array}{l}{b}^{2}-2{b}^{2}+c=3\\ 4=4-4b+c\end{array}\right.$,
解得$\left\{\begin{array}{l}b=1\\ c=4\end{array}\right.$或$\left\{\begin{array}{l}b=3\\ c=12\end{array}\right.$.
函数f(x)的解析式:f(x)=x2-2x+4或f(x)=x2-6x+12..
点评 此题主要考查了待定系数法求二次函数解析式以及求二次函数顶点坐标,熟练掌握待定系数法是关键.


科目:高中数学 来源: 题型:解答题
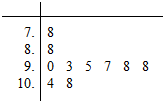 某射击爱好者想提高自己的射击水平,制订了了一个训练计划,为了了解训练效果,执行训练计划前射击了10发子弹(每发满分为10.9环),计算出成绩中位数为9.65环,总成绩为95.1环,成绩标准差为1.09环,执行训练计划后也射击了10发子弹,射击成绩茎叶图如图所示.
某射击爱好者想提高自己的射击水平,制订了了一个训练计划,为了了解训练效果,执行训练计划前射击了10发子弹(每发满分为10.9环),计算出成绩中位数为9.65环,总成绩为95.1环,成绩标准差为1.09环,执行训练计划后也射击了10发子弹,射击成绩茎叶图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3-2$\sqrt{2}$)R | B. | (4-2$\sqrt{3}$)R | C. | (5-2$\sqrt{6}$)R | D. | (6-2$\sqrt{7}$)R |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com