解:(1)函数y=cos2x-4asinx-3a=1-2sin
2x-4asinx-3a=-2 (sinx+a)
2+2a
2-3a+1.
令sinx=t∈[-1,1],则 函数y=-2(t+a)
2+2a
2-3a+1.
当-a<-1 时,即 a>1 时,则t=-1时,M(a)=-2(-1+a)
2+2a
2-3a+1=a-1.
当-1≤-a≤1 时,即 1≥a≥-1时,则t=-a时,M(a)=2a
2-3a+1.
当-a>1 时,即 a<-1时,则t=1时,M(a)=-2(1+a)
2+2a
2-3a+1=-7a-1.
综上,
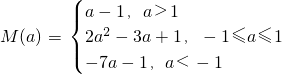
.
(2)当a>1时,M(a)=a-1,最小值大于0.
当-1≤a≤1时,M(a)=2a
2-3a+1,最小值为-

.
当a<-1时,M(a)=-7a-1>6.
综上可得 M(a)的最小值为
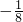
.
分析:(1)利用三角函数的恒等变换化简函数y的解析式为-2 (sinx+a)
2+2a
2-3a+1,令sinx=t∈[-1,1],则 函数y=-2(t+a)
2+2a
2-3a+1.利用二次函数的性质,求出函数在闭区间[-1,1]的最大值.
(2)当a>1时,M(a)=a-1,最小值大于0. 当-1≤a≤1时,M(a)=2a
2-3a+1,最小值为-

.当a<-1时,M(a)=-7a-1>6.综合可得M(a)的最小值.
点评:本题主要考查三角函数的恒等变换及化简求值,二次函数的性质,复合函数的单调性的应用,体现了分类讨论的数学思想,属于中档题.

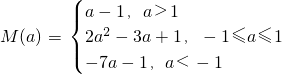 .
. .
.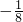 .
. .当a<-1时,M(a)=-7a-1>6.综合可得M(a)的最小值.
.当a<-1时,M(a)=-7a-1>6.综合可得M(a)的最小值.

 通城学典默写能手系列答案
通城学典默写能手系列答案