(1)a

=2
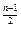
,n为奇数;a

=2
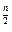
,n为偶数;
(2)S

=2
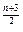
-3,n为奇数;S

=3(2
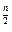
-1),n为偶数;
当n为奇数时,,
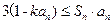
3(1-ka

)
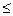
(2
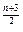
-3)a

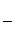
k
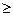
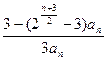
K
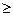
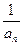
-(
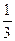
2
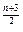
-1)=
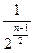
-
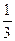
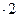
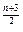
+1
F(n)=
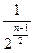
-
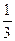
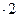
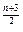
+1单调递减;F(1)=
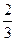
最大;
K
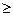
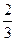
当n为偶数时,
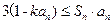
3(1-ka

)
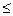
3(2
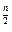
-

1)a

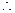
k
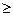
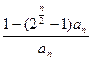
=
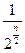
-2
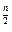
+1
F(n)=
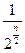
-2
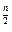
+1单调递减,所以n=2时F(2)=-0.5
K
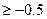
综合上面可得k
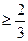
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(本题13分)
已知等比数列
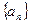
的前
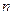
项和是
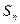
,满足
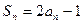
.
(Ⅰ)求数列
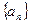
的通项
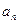
及前
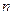
项和
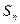
;
(Ⅱ)若

数列
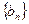
满足
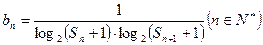
,求数列
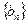
的前
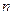
项和
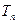
;
(Ⅲ)若对任意的
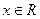
,恒有
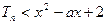
成立,求实数
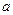
的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
.若
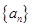
是等差数列,公差
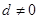
,
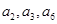
成等比数列,则公比为 ( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
((本小题满分12分)
设
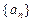
为等差数列,
Sn为数列
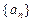
的前
n项和,已知
S7=7,
S15=75,
Tn为数列
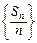
的前
n项和,求
Tn.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
等差数列
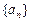
中,
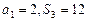

(1)求数列
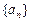
的通项公式;
(2)令
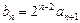
,求数列
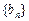
的前
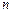
项和
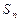
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知数列
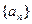
为等差数列,若
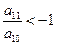
,且它们的前
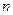
项和
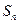
有最大值,则使得
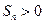
的
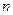
的最大

值为 ( )
| A.11 | B.19  | C.20 | D.21 |
查看答案和解析>>

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案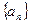 的前
的前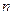 项和是
项和是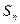 ,满足
,满足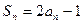 .
.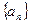 的通项
的通项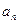 及前
及前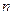 项和
项和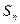 ;
; 数列
数列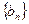 满足
满足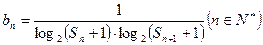 ,求数列
,求数列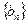 的前
的前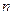 项和
项和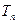 ;
;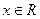 ,恒有
,恒有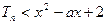 成立,求实数
成立,求实数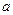 的取值范围.
的取值范围.