
【题目】如图,平面![]() 平面
平面![]() ,四边形
,四边形![]() 和
和![]() 是全等的等腰梯形,其中
是全等的等腰梯形,其中![]() ,且
,且![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 是
是![]() 的中点.
的中点.

(I)请在图中所给的点中找出两个点,使得这两个点所在直线与平面![]() 垂直,并给出证明;
垂直,并给出证明;
(II)求二面角![]() 的余弦值;
的余弦值;
(III)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?如果存在,求出
?如果存在,求出![]() 的长度,如果不存在,请说明理由.
的长度,如果不存在,请说明理由.
【答案】(I)见解析;(II)![]() ;(III)见解析.
;(III)见解析.
【解析】试题分析: ![]() 法一:向量法,分别以边
法一:向量法,分别以边![]() ,
, ![]() ,
, ![]() 所在直线为
所在直线为![]() ,
, ![]() ,
, ![]() 轴,给出相应点坐标,证明
轴,给出相应点坐标,证明![]() ,
, ![]() 法二:先证
法二:先证![]()
![]() 接着证明所以
接着证明所以![]()
![]() 平面
平面![]() 即
即![]() 最后证得结果(2)要求二面角的平面角的余弦值就先求得平面
最后证得结果(2)要求二面角的平面角的余弦值就先求得平面![]() 的法向量,利用公式即可算出结果(3)法一:借助向量假设存在,计算可得
的法向量,利用公式即可算出结果(3)法一:借助向量假设存在,计算可得![]() 矛盾,故不存在;法二:假设存在点
矛盾,故不存在;法二:假设存在点![]() ,证得平面
,证得平面![]() 平面
平面![]() ,即有
,即有![]() 为平行四边形,所以
为平行四边形,所以![]() ,矛盾
,矛盾
解析:法一:向量法
(I)![]() ,
, ![]() 点为所求的点.
点为所求的点.
证明如下:
因为四边形![]() 是等腰梯形,点
是等腰梯形,点![]() 为
为![]() 的中点,点
的中点,点![]() 是
是![]() 的中点,
的中点,
所以![]() .
.
又平面![]()
![]() 平面
平面![]() ,平面
,平面![]()
![]() 平面
平面![]() =
= ![]() ,
,
所以![]()
![]() 平面
平面![]()
同理取![]() 的中点
的中点![]() ,则
,则![]()
![]() 平面
平面![]() .
.
分别以边![]() ,
, ![]() ,
, ![]() 所在直线为
所在直线为![]() ,
, ![]() ,
, ![]() 轴,建立如图所示的空间直角坐标系.
轴,建立如图所示的空间直角坐标系.
由![]() ,得
,得![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
则![]() ,
, ![]() ,
, ![]() .
.
所以![]() ,
, ![]()
又![]() ,
,
所以![]() 平面
平面![]()
(II)由(I)知平面![]() 的一个法向量为
的一个法向量为![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则
![]() 即
即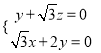
令![]() ,则
,则![]() ,
, ![]()
所以![]()
所以![]()
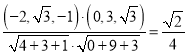
所以二面角![]() 的余弦值为
的余弦值为![]()
(III)假设存在点![]() ,使得
,使得![]()
![]() 平面
平面![]() .
.
设![]()
所以![]()
![]() ,所以
,所以![]()
而计算可得![]()
这与![]() 矛盾
矛盾
所以在线段![]() 上不存在点
上不存在点![]() ,使得
,使得![]()
![]() 平面
平面![]()
法二:(I)证明如下:
因为四边形![]() 是等腰梯形,点
是等腰梯形,点![]() 为
为![]() 的中点,点
的中点,点![]() 是
是![]() 的中点,
的中点,
所以![]()
![]()
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]()
![]() 平面
平面![]()
因为![]()
![]() 平面
平面![]() ,所以
,所以![]() ,
,
又![]() ,且
,且![]() ,
,
所以![]() 为菱形,所以
为菱形,所以![]()
因为![]() ,
,
所以![]() 平面
平面![]() .
.
(III)假设存在点![]() ,使得
,使得![]() 平面
平面![]()
由![]() ,所以
,所以![]() 为平行四边形,
为平行四边形,
所以![]()
因为![]() 平面
平面![]()
所以![]() 平面
平面![]()
又![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() ,
,
所以![]() 为平行四边形,所以
为平行四边形,所以![]() ,矛盾
,矛盾
所以不存在点![]() ,使得
,使得![]() 平面
平面![]()


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:
【题目】如图是一段圆锥曲线,曲线与两个坐标轴的交点分别是![]() .
.

(1)若该曲线为椭圆(中心为原点,对称轴为坐标轴)的一部分,设直线![]() 过点
过点![]() 且斜率是
且斜率是![]() ,求直线
,求直线![]() 与该段曲线的公共点的坐标.
与该段曲线的公共点的坐标.
(2)若该曲线为抛物线的一部分,求原抛物线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂利用辐射对食品进行灭菌消毒,现准备在该厂附近建一职工宿舍,并对宿舍进行防辐射处理,建房防辐射材料的选用与宿舍到工厂距离有关.若建造宿舍的所有费用![]() (万元)和宿舍与工厂的距离
(万元)和宿舍与工厂的距离![]() 的关系为:
的关系为: ![]() .为了交通方便,工厂与宿舍之间还要修一条简易便道,已知修路每公里成本为
.为了交通方便,工厂与宿舍之间还要修一条简易便道,已知修路每公里成本为![]() 万元,工厂一次性补贴职工交通费
万元,工厂一次性补贴职工交通费![]() 万元.设
万元.设![]() 为建造宿舍、修路费用与给职工的补贴之和.
为建造宿舍、修路费用与给职工的补贴之和.
⑴求![]() 的表达式;
的表达式;
⑵宿舍应建在离工厂多远处,可使总费用![]() 最小,并求最小值.
最小,并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选做题】本题包括A、B、C、D四小题,请选定其中两小题,并在相应的答题区域内作答.若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.
(1)A.【选修4—1几何证明选讲】
如图,在△ABC中,∠ABC=90°,BD⊥AC , D为垂足,E是BC的中点,求证:∠EDC=∠ABD.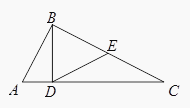
(2)B.【选修4—2:矩阵与变换】
已知矩阵A= ![]() 矩阵B的逆矩阵B﹣1=
矩阵B的逆矩阵B﹣1= 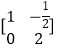 ,求矩阵AB.
,求矩阵AB.
(3)【选修4—4:坐标系与参数方程】在平面直角坐标系xOy中,已知直线l的参数方程为 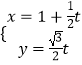 (t为参数),椭圆C的参数方程为
(t为参数),椭圆C的参数方程为 ![]() (
( ![]() 为参数).设直线l与椭圆C相交于A , B两点,求线段AB的长.
为参数).设直线l与椭圆C相交于A , B两点,求线段AB的长.
(4)D. 设a>0,|x﹣1|< ![]() ,|y﹣2|<
,|y﹣2|< ![]() ,求证:|2x+y﹣4|<a.
,求证:|2x+y﹣4|<a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)△ABC中,角A,B,C所对的边分别为a,b,c.已知a=3,cos A=![]() ,B=A+
,B=A+![]() .
.
(1)求b的值;
(2)求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海关对同时从![]() 三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示,工作人员用分层抽样的方法从这些商品中共抽取6件进行检测.
三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示,工作人员用分层抽样的方法从这些商品中共抽取6件进行检测.
地区 |
|
|
|
数量 | 50 | 150 | 100 |
(1)求这6件样品中来自![]() 各地区商品的数量;
各地区商品的数量;
(2)若在这6件样品中随机抽取2件送往甲机构进一步检测,求这2件商品来自相同地区的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=2 ![]() sin(π﹣x)sinx﹣(sinx﹣cosx)2 .
sin(π﹣x)sinx﹣(sinx﹣cosx)2 .
(1)求f(x)的单调递增区间;
(2)把y=f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移 ![]() 个单位,得到函数y=g(x)的图象,求g(
个单位,得到函数y=g(x)的图象,求g( ![]() )的值.
)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com