
 ,某植物研究所进行该种子的发芽实验,每次实验种一料种子,每次实验结果相互独立.假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.若该研究所共进行四次实验,设ξ表示四次实验结束时实验成功的次数与失败的次数之差的绝对值;
,某植物研究所进行该种子的发芽实验,每次实验种一料种子,每次实验结果相互独立.假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.若该研究所共进行四次实验,设ξ表示四次实验结束时实验成功的次数与失败的次数之差的绝对值;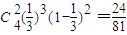 .P(ξ=2)=
.P(ξ=2)=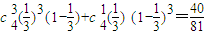 .p(ξ=4)=
.p(ξ=4)=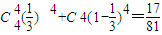 ,由此能求出随机变量ξ的数学期望.
,由此能求出随机变量ξ的数学期望.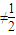 },说明事件A不发生.由此能求出事件A发生的概率P(A).
},说明事件A不发生.由此能求出事件A发生的概率P(A).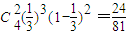 .
.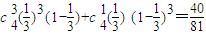 .
.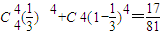 ,(6分)
,(6分)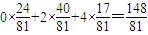 .
.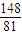 .(7分)
.(7分)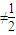 },
},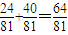 .(12分)
.(12分)

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| 1 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 ,某植物研究所进行该种子的发芽实验,每次实验种一料种子,每次实验结果相互独立.假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.若该研究所共进行四次实验,设ξ表示四次实验结束时实验成功的次数与失败的次数之差的绝对值;
,某植物研究所进行该种子的发芽实验,每次实验种一料种子,每次实验结果相互独立.假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.若该研究所共进行四次实验,设ξ表示四次实验结束时实验成功的次数与失败的次数之差的绝对值;查看答案和解析>>
科目:高中数学 来源:2012年华约自主招生数学全真模拟试卷Advanced Assessment for Admission(AAA)(解析版) 题型:解答题
 ,某植物研究所进行该种子的发芽实验,每次实验种一料种子,每次实验结果相互独立.假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.若该研究所共进行四次实验,设ξ表示四次实验结束时实验成功的次数与失败的次数之差的绝对值;
,某植物研究所进行该种子的发芽实验,每次实验种一料种子,每次实验结果相互独立.假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.若该研究所共进行四次实验,设ξ表示四次实验结束时实验成功的次数与失败的次数之差的绝对值;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com