
【题目】正△ABC的边长为2, CD是AB边上的高,E、F分别是AC和BC的中点(如图(1)).现将△ABC沿CD翻成直二面角A-DC-B(如图(2)).在图(2)中:
(1)求证:AB∥平面DEF;
(2)在线段BC上是否存在一点P,使AP⊥DE?证明你的结论;
(3)求二面角E-DF-C的余弦值.

【答案】(1) 见解析.(2) 见解析.(3) ![]() .
.
【解析】试题分析:(Ⅰ)由E、F分别是AC、BC的中点,得EF∥AB,由此能证明AB∥平面DEF;(Ⅱ)以点D为坐标原点,以直线DB、DC、DA分别为x轴、y轴、z轴,建立空间直角坐标系.利用向量法能在线段BC上存在点P,使AP⊥DE;(Ⅲ)分别求出平面CDF的法向量和平面EDF的法向量,利用同向量法能求出二面角E-DF-C的平面角的余弦值
试题解析:(1)证明:在△ABC中,因为E、F分别是AC、BC的中点,
所以EF∥AB.
又AB平面DEF,EF平面DEF,
所以AB∥平面DEF.
(2)以点D为坐标原点,以直线DB、DC、DA分别为x轴、y轴、z轴建立空间直角坐标系(图略).则A(0,0,1),B(1,0,0),C(0, ![]() ,0),E(0,
,0),E(0, ![]() ,
, ![]() ),F(
),F(![]() ,
, ![]() ,0),
,0),![]() =(1,0,-1),
=(1,0,-1),![]() =(-1,
=(-1, ![]() ,0),
,0),![]() =(0,
=(0, ![]() ,
, ![]() ),
),![]() =(
=(![]() ,
, ![]() ,0).
,0).
设![]() =λ
=λ![]() ,则
,则![]() =
=![]() +
+![]() =(1-λ,
=(1-λ, ![]() λ,-1),
λ,-1),
注意到AP⊥DE![]() ·
·![]() =0λ=
=0λ=![]()
![]() =
=![]()
![]() ,
,
所以在线段BC上存在点P,使AP⊥DE.
(3)平面CDF的一个法向量![]() =(0,0,1),设平面EDF的法向量为n=(x,y,z),
=(0,0,1),设平面EDF的法向量为n=(x,y,z),
则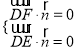 ,即
,即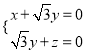 ,取n=(3,-
,取n=(3,- ![]() ,3),
,3),
cos〈![]() ,n〉=
,n〉=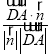 =
=![]() ,
,
所以二面角EDFC的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,椭圆C过点
中,椭圆C过点![]() ,焦点
,焦点![]() ,圆O的直径为
,圆O的直径为![]() .
.

(1)求椭圆C及圆O的方程;
(2)设直线l与圆O相切于第一象限内的点P.
①若直线l与椭圆C有且只有一个公共点,求点P的坐标;
②直线l与椭圆C交于![]() 两点.若
两点.若![]() 的面积为
的面积为![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 棱的中点.
棱的中点.

(1)证明![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)设点![]() 在线段
在线段![]() 上,且直线
上,且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数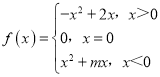 是奇函数,则实数m的值是______;若函数f(x)在区间[-1,a-2]上满足对任意x1≠x2,都有
是奇函数,则实数m的值是______;若函数f(x)在区间[-1,a-2]上满足对任意x1≠x2,都有![]() 成立,则实数a的取值范围是______.
成立,则实数a的取值范围是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为奇函数.
为奇函数.
(1)求a的值,并证明![]() 是R上的增函数;
是R上的增函数;
(2)若关于t的不等式f(t2-2t)+f(2t2-k)<0的解集非空,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:
①若![]() 是定义在
是定义在![]() 上的偶函数,且在
上的偶函数,且在![]() 上是增函数,
上是增函数,![]() ,则
,则![]() ;
;
②若锐角![]() 、
、![]() 满足c
满足c![]() ,则
,则![]() ;
;
③若![]() ,则
,则![]() 对
对![]() 恒成立;
恒成立;
④要得到![]() 的图像,只需将
的图像,只需将![]() 的图像向右平移
的图像向右平移![]() 个单位:
个单位:
其中真命题的个数有( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资公司计划投资![]() ,
,![]() 两种金融产品,根据市场调查与预测,
两种金融产品,根据市场调查与预测,![]() 产品的利润
产品的利润![]() 与投资金额
与投资金额![]() 的函数关系为
的函数关系为![]() ,
,![]() 产品的利润
产品的利润![]() 与投资金额
与投资金额![]() 的函数关系为
的函数关系为![]() .(注:利润与投资金额单位:万元)
.(注:利润与投资金额单位:万元)
(1)该公司已有100万元资金,并全部投入![]() ,
,![]() 两种产品中,其中
两种产品中,其中![]() 万元资金投入
万元资金投入![]() 产品,试把
产品,试把![]() ,
,![]() 两种产品利润总和表示为
两种产品利润总和表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)试问:怎样分配这100万元资金,才能使公司获得最大利润?其最大利润为多少万元?
【答案】(1)![]() ;(2)20,28.
;(2)20,28.
【解析】
(1)设投入![]() 产品
产品![]() 万元,则投入
万元,则投入![]() 产品
产品![]() 万元,根据题目所给两个产品利润的函数关系式,求得两种产品利润总和的表达式.(2)利用基本不等式求得利润的最大值,并利用基本不等式等号成立的条件求得资金的分配方法.
万元,根据题目所给两个产品利润的函数关系式,求得两种产品利润总和的表达式.(2)利用基本不等式求得利润的最大值,并利用基本不等式等号成立的条件求得资金的分配方法.
(1)其中![]() 万元资金投入
万元资金投入![]() 产品,则剩余的
产品,则剩余的![]() (万元)资金投入
(万元)资金投入![]() 产品,
产品,
利润总和为:![]()
![]() ,
,
(2)因为![]() ,
,![]()
所以由基本不等式得:![]() ,
,
当且仅当![]() 时,即:
时,即:![]() 时获得最大利润28万.
时获得最大利润28万.
此时投入A产品20万元,B产品80万元.
【点睛】
本小题主要考查利用函数求解实际应用问题,考查利用基本不等式求最大值,属于中档题.
【题型】解答题
【结束】
20
【题目】已知曲线![]() .
.
(1)求曲线在![]() 处的切线方程;
处的切线方程;
(2)若曲线在点![]() 处的切线与曲线
处的切线与曲线![]() 相切,求
相切,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com