
【题目】闰月年指农历里有闰月的年份,比如2020年是闰月年,4月23日至5月22日为农历四月,5月23日至6月20日为农历闰四月.农历置闰月是为了农历年的平均长度接近回归年:农历年中的朔望月的平均长度为29.5306日,![]() 日,回归年的总长度为365.2422日,两者相差10.875日.因此,每19年相差206.625日,约等于7个朔望月.这样每19年就有7个闰月年.以下是1640年至1694年间所有的闰月年:
日,回归年的总长度为365.2422日,两者相差10.875日.因此,每19年相差206.625日,约等于7个朔望月.这样每19年就有7个闰月年.以下是1640年至1694年间所有的闰月年:
1640 | 1642 | 1645 | 1648 | 1651 | 1653 | 1656 |
1659 | 1661 | 1664 | 1667 | 1670 | 1672 | 1675 |
1678 | 1680 | 1 683 | 1686 | 1689 | 1691 | 1694 |
则从2020年至2049年,这30年间闰月年的个数为( )
A.10B.11C.12D.13
科目:高中数学 来源: 题型:
【题目】足球运动被誉为“世界第一运动”.为推广足球运动,某学校成立了足球社团由于报名人数较多,需对报名者进行“点球测试”来决定是否录取,规则如下:
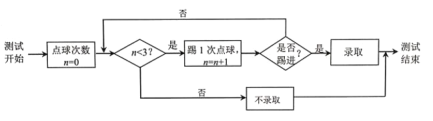
(1)下表是某同学6次的训练数据,以这150个点球中的进球频率代表其单次点球踢进的概率.为加入足球社团,该同学进行了“点球测试”,每次点球是否踢进相互独立,将他在测试中所踢的点球次数记为![]() ,求
,求![]() ;
;
![]()
(2)社团中的甲、乙、丙三名成员将进行传球训练,从甲开始随机地将球传给其他两人中的任意一人,接球者再随机地将球传给其他两人中的任意一人,如此不停地传下去,且假定每次传球都能被接到.记开始传球的人为第1次触球者,接到第n次传球的人即为第![]() 次触球者
次触球者![]() ,第n次触球者是甲的概率记为
,第n次触球者是甲的概率记为![]() .
.
(i)求![]() ,
,![]() ,
,![]() (直接写出结果即可);
(直接写出结果即可);
(ii)证明:数列![]() 为等比数列.
为等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,我国电子商务行业迎来了蓬勃发展的新机遇,但是电子商务行业由于缺乏监管,服务质量有待提高.某部门为了对本地的电商行业进行有效监管,调查了甲、乙两家电商的某种同类产品连续十天的销售额(单位:万元),得到如下茎叶图:
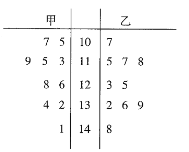
(1)根据茎叶图判断甲、乙两家电商对这种产品的销售谁更稳定些?
(2)如果日销售额超过平均销售额,相应的电商即被评为优,根据统计数据估计两家电商一个月(按30天计算)被评为优的天数各是多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)求 函数![]() 的单调区间;
的单调区间;
(2)定义:对于函数![]() ,若存在
,若存在![]() ,使
,使![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 的不动点. 如果函数
的不动点. 如果函数![]() 存在两个不同的不动点,求实数
存在两个不同的不动点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的右准线为直线
的右准线为直线![]() ,左顶点为
,左顶点为![]() ,右焦点为
,右焦点为![]() . 已知斜率为2的直线
. 已知斜率为2的直线![]() 经过点
经过点![]() ,与椭圆
,与椭圆![]() 相交于
相交于![]() 两点,且
两点,且![]() 到直线
到直线![]() 的距离为
的距离为![]()
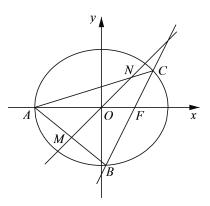
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若过![]() 的直线
的直线![]() 与直线
与直线![]() 分别相交于
分别相交于![]() 两点,且
两点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小张上班从家到公司开车有两条线路,所需时间(分钟)随交通堵塞状况有所变化,其概率分布如下表所示:
所需时间(分钟) | 30 | 40 | 50 | 60 |
线路一 | 0.5 | 0.2 | 0.2 | 0.1 |
线路二 | 0.3 | 0.5 | 0.1 | 0.1 |
则下列说法正确的是( )
A.任选一条线路,“所需时间小于50分钟”与“所需时间为60分钟”是对立事件
B.从所需的平均时间看,线路一比线路二更节省时间
C.如果要求在45分钟以内从家赶到公司,小张应该走线路一
D.若小张上、下班走不同线路,则所需时间之和大于100分钟的概率为0.04
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.在做回归分析时,残差图中残差点分布的带状区域的宽度越窄表示回归效果越差
B.某地气象局预报:6月9日本地降水概率为90%,结果这天没下雨,这表明天气预报并不科学
C.回归分析模型中,残差平方和越小,说明模型的拟合效果越好
D.在回归直线方程![]() 中,当解释变量每增加1个单位时,预报变量多增加0.1个单位
中,当解释变量每增加1个单位时,预报变量多增加0.1个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社会机构为了调查对手机游戏的兴趣与年龄的关系,通过问卷调查,整理数据得如下![]() 列联表:
列联表:
40岁以下 | 40岁以上 | 合计 | |
很兴趣 | 30 | 15 | 45 |
无兴趣 | 20 | 35 | 55 |
合计 | 50 | 50 | 100 |
(1)根据列联表,能否有![]() 的把握认为对手机游戏的兴趣程度与年龄有关?
的把握认为对手机游戏的兴趣程度与年龄有关?
(2)若已经从![]() 岁以下的被调查者中用分层抽样的方式抽取了
岁以下的被调查者中用分层抽样的方式抽取了![]() 名,现从这
名,现从这![]() 名被调查者中随机选取
名被调查者中随机选取![]() 名,求这
名,求这![]() 名被调查者中恰有
名被调查者中恰有![]() 名对手机游戏无兴趣的概率.
名对手机游戏无兴趣的概率.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.84 | 6.635 | 10.828 |
(注:参考公式: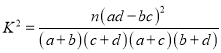 ,其中
,其中![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com