
已知二面角 —
— —β的大小为45°,m,n为异面直线,且m
—β的大小为45°,m,n为异面直线,且m ,n
,n β,则m,n所成角的大小为
β,则m,n所成角的大小为
A、135° B、90° C、60° D、45°
科目:高中数学 来源: 题型:
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
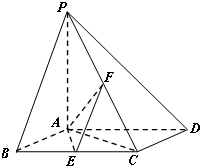 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在正三棱柱ABC-A1B1C1中,点M为侧棱AA1上一动点,已知△BCM面积的最大值是2
如图,在正三棱柱ABC-A1B1C1中,点M为侧棱AA1上一动点,已知△BCM面积的最大值是2| 3 |
| π |
| 3 |
A、3
| ||
B、2
| ||
C、
| ||
D、3
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD,G,H分别是DF,BE的中点.
如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD,G,H分别是DF,BE的中点.查看答案和解析>>
科目:高中数学 来源:2009-2010学年度新课标高二上学期数学单元测试4 题型:选择题
(理)已知二面角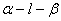 的平面角为
的平面角为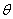 ,PA
,PA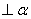 ,PB
,PB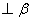 ,A,B为垂足,且PA=4,PB=5,设A、B到二面角的棱
,A,B为垂足,且PA=4,PB=5,设A、B到二面角的棱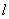 的距离为别为
的距离为别为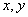 ,当
,当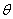 变化时,点
变化时,点 的轨迹是下列图形中的 ( )
的轨迹是下列图形中的 ( )
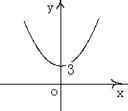
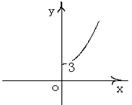
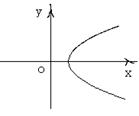
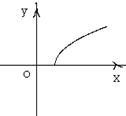
A B C D
(文)函数 上取得最大值时,x的值为 ( )
上取得最大值时,x的值为 ( )
A.0 B.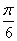 C.
C.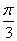 D.
D.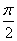
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com