
【题目】已知![]() ,设函数
,设函数![]() ,
,![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)是否存在整数![]() ,对于任意
,对于任意![]() ,关于
,关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有唯一实数解?若存在,求
上有唯一实数解?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)当![]() 时,单调递减区间是
时,单调递减区间是![]() ,当
,当![]() 时,单调递减区间是
时,单调递减区间是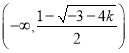 和
和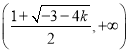 ,单调递增区间是
,单调递增区间是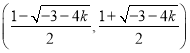
(2)存在,![]()
【解析】
(1)根据题意单调![]() ,求导
,求导![]() ,令
,令![]() ,分
,分![]() ,
,![]() 两者情况讨论求解.
两者情况讨论求解.
(2)先求![]() 时,
时,![]() 的根,得到区间
的根,得到区间![]() ,当
,当![]() 时,求导
时,求导 ![]() ,讨论
,讨论![]() ,
,![]() 时,
时,![]() ,当
,当![]() 且
且![]() ,利用等比数列求和公式得到
,利用等比数列求和公式得到![]() ,分析得
,分析得![]() ,得到
,得到![]() 在R上是减函数,再论证
在R上是减函数,再论证![]() ,
,![]() ,利用零点存在定理得到结论.
,利用零点存在定理得到结论.
(1)因为![]() ,
,
所以![]() ,
,![]() ,
,
令![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() 在R上单调递减,
在R上单调递减,
当![]() 时,
时,![]() ,方程
,方程![]() 有两个不等根,
有两个不等根,
![]()
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 在
在![]()
![]() 递减,在
递减,在![]() 上递增.
上递增.
综上:当![]() 时,
时,![]() 的减区间是
的减区间是![]() ,
,
当![]() 时,
时, ![]() 的减区间是
的减区间是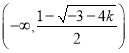 ,
,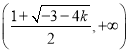 ,增区间是
,增区间是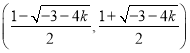 .
.
(2)存在![]() ,对于任意
,对于任意![]() ,关于
,关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有唯一实数解,理由如下:
上有唯一实数解,理由如下:
当![]() 时,
时,![]() ,令
,令![]() ,解得
,解得![]() ,
,
所以关于![]() 的方程
的方程![]() 有唯一实数解.
有唯一实数解.
当![]() 时,
时,![]() ,
,![]() ,
,
若![]() ,则
,则![]() ,
,
若![]() ,
,![]() ,
,
若![]() 且
且![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,所以
,所以![]()
当![]() 时,
时,![]() ,所以
,所以![]() ,
,
故![]() 在R上是减函数.
在R上是减函数.
又![]() ,
,
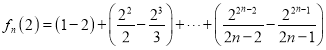 ,
,
![]() ,
,
![]() ,
,
所以方程![]() 在区间
在区间![]() 上有唯一实数解.
上有唯一实数解.
综上:对于任意![]() ,关于
,关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有唯一实数解,所以
上有唯一实数解,所以![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,上顶点为A,过
,上顶点为A,过![]() 的直线
的直线![]() 与y轴交于点M,满足
与y轴交于点M,满足![]() (O为坐标原点),且直线l与直线
(O为坐标原点),且直线l与直线![]() 之间的距离为
之间的距离为![]() .
.
(1)求椭圆C的方程;
(2)在直线![]() 上是否存在点P,满足
上是否存在点P,满足![]() ?存在,指出有几个这样的点(不必求出点的坐标);若不存在,请说明理由.
?存在,指出有几个这样的点(不必求出点的坐标);若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,直线
,直线![]() 过焦点
过焦点![]() 且与抛物线交于
且与抛物线交于![]() 、
、![]() 两点,当直线
两点,当直线![]() 的倾斜角为30°时,
的倾斜角为30°时,![]() .
.
(1)求抛物线方程.
(2)在平面直角坐标系![]() 中,是否存在定点
中,是否存在定点![]() ,当直线
,当直线![]() 绕
绕![]() 旋转时始终都满足
旋转时始终都满足![]() 平分
平分![]() .若存在,求出
.若存在,求出![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一对夫妇为了给他们的独生孩子支付将来上大学的费用,从孩子一周岁生日开始,每年到银行储蓄![]() 元一年定期,若年利率为
元一年定期,若年利率为![]() 保持不变,且每年到期时存款(含利息)自动转为新的一年定期,当孩子18岁生日时不再存入,将所有存款(含利息)全部取回,则取回的钱的总数为
保持不变,且每年到期时存款(含利息)自动转为新的一年定期,当孩子18岁生日时不再存入,将所有存款(含利息)全部取回,则取回的钱的总数为![]()
![]()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 的离心率为
的离心率为![]() ,以椭圆
,以椭圆![]() 的上顶点
的上顶点![]() 为圆心作圆,
为圆心作圆,
![]() ,圆
,圆![]() 与椭圆
与椭圆![]() 在第一象限交于点
在第一象限交于点![]() ,在第二象限交于点
,在第二象限交于点![]() .
.
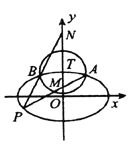
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的最小值,并求出此时圆
的最小值,并求出此时圆![]() 的方程;
的方程;
(3)设点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的一点,且直线
的一点,且直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() 为坐标原点,求证:
为坐标原点,求证:
![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】欧阳修《卖油翁》中写道:(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌滴沥之,自钱孔入,而钱不湿.已知铜钱是直径为4 cm的圆面,中间有边长为1 cm的正方形孔,若随机向铜钱上滴一滴油(油滴整体落在铜钱内),则油滴整体(油滴是直径为0.2 cm的球)正好落入孔中的概率是_____.(不作近似计算)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个,补充在下面的问题中,并解决该问题.
这三个条件中任选一个,补充在下面的问题中,并解决该问题.
已知![]() 的内角
的内角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() ______________,
______________,![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年反映社会现实的电影《我不是药神》引起了很大的轰动,治疗特种病的创新药研发成了当务之急.为此,某药企加大了研发投入,市场上治疗一类慢性病的特效药品![]() 的研发费用
的研发费用![]() (百万元)和销量
(百万元)和销量![]() (万盒)的统计数据如下:
(万盒)的统计数据如下:
研发费用 | 2 | 3 | 6 | 10 | 13 | 15 | 18 | 21 |
销量 | 1 | 1 | 2 | 2.5 | 3.5 | 3.5 | 4.5 | 6 |
(1)求![]() 与
与![]() 的相关系数
的相关系数![]() 精确到0.01,并判断
精确到0.01,并判断![]() 与
与![]() 的关系是否可用线性回归方程模型拟合?(规定:
的关系是否可用线性回归方程模型拟合?(规定:![]() 时,可用线性回归方程模型拟合);
时,可用线性回归方程模型拟合);
(2)该药企准备生产药品![]() 的三类不同的剂型
的三类不同的剂型![]() ,
,![]() ,
,![]() ,并对其进行两次检测,当第一次检测合格后,才能进行第二次检测.第一次检测时,三类剂型
,并对其进行两次检测,当第一次检测合格后,才能进行第二次检测.第一次检测时,三类剂型![]() ,
,![]() ,
,![]() 合格的概率分别为
合格的概率分别为![]() ,
,![]() ,
,![]() ,第二次检测时,三类剂型
,第二次检测时,三类剂型![]() ,
,![]() ,
,![]() 合格的概率分别为
合格的概率分别为![]() ,
,![]() ,
,![]() .两次检测过程相互独立,设经过两次检测后
.两次检测过程相互独立,设经过两次检测后![]() ,
,![]() ,
,![]() 三类剂型合格的种类数为
三类剂型合格的种类数为![]() ,求
,求![]() 的数学期望.
的数学期望.
附:(1)相关系数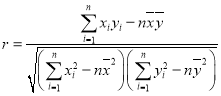
(2)![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年是新中国成立七十周年,新中国成立以来,我国文化事业得到了充分发展,尤其是党的十八大以来,文化事业发展更加迅速,下图是从2013 年到 2018 年六年间我国公共图书馆业机构数(个)与对应年份编号的散点图(为便于计算,将 2013 年编号为 1,2014 年编号为 2,…,2018年编号为 6,把每年的公共图书馆业机构个数作为因变量,把年份编号从 1 到 6 作为自变量进行回归分析),得到回归直线![]() ,其相关指数
,其相关指数![]() ,给出下列结论,其中正确的个数是( )
,给出下列结论,其中正确的个数是( )

①公共图书馆业机构数与年份的正相关性较强
②公共图书馆业机构数平均每年增加13.743个
③可预测 2019 年公共图书馆业机构数约为3192个
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com