Question

【题目】已知 的内切圆切边于点， 而是边上的任意内点.设和的内切圆圆心分别是和.

（1）求证：∠I1DI2 =90°（即、、、四点共圆）；

（2）设、、、四点所在的圆周的半径为， 而的内切圆半径为，试求的取值范围（取遍各种形状的三角形，点取遍边上的每一个内点）.

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）如图，联结 、、.由平分及平 分，易 知=90 °.

故只须证明、、 、四点共圆， 而这只须证明.

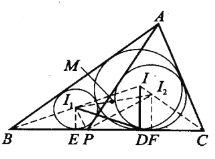
设切于点，则.只须证明，

亦只须证明，即. ①

设切于点，联结，则.

由于，故.

从而，.

所以， .

于是，，即. ②

由式①、②可知， 只须证明. ③

欲证式③， 只须证明. ④

由切线长相等得，

即式④、③确实成立.

再由式 ②可推出式 ①成立， 从而，，即、、 、四点共圆.

因此，.

（2）由（1）知、、 、四点共圆，，所以，.

显然，、、三点共线，、、也三点共线，且

.

取的中点，则是、、 、四点所在圆周的圆心，为该圆直径.由于 ，所以，点必在⊙的内部.从而，必不是直径.

于是，，即.故.

若固定不变，且，当，且为的中点，则，即.

若固定不变，当且为上的定点，，

（定值），这时，.

再由几何图形变化的连续性可知，可取遍开区间内的所有值.

综上可知， 的取值范围是.