
【题目】已知| ![]() |=4,|
|=4,| ![]() |=2,且
|=2,且 ![]() 与
与 ![]() 夹角为120°求:
夹角为120°求:
(1)( ![]() ﹣2
﹣2 ![]() )(
)( ![]() +
+ ![]() );
);
(2)![]() 在
在 ![]() 上的投影;
上的投影;
(3)![]() 与
与 ![]() +
+ ![]() 的夹角.
的夹角.
科目:高中数学 来源: 题型:
【题目】如图ABCD﹣A1B1C1D1是长方体,O是B1D1的中点,直线AC1交平面CB1D1于点M,则下列结论正确的是( ) 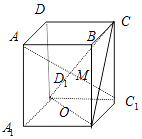
A.C,M,O三点共线
B.C,M,O,A1不共面
C.A,M,O,C不共面
D.B,M,O,B1共面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() 的定义域为A,函数y=log2(a﹣x)的定义域为B.
的定义域为A,函数y=log2(a﹣x)的定义域为B.
(1)若AB,求实数a的取值范围;
(2)设全集为R,若非空集合(RB)∩A的元素中有且只有一个是整数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga ![]() (a>0,a≠1)是奇函数.
(a>0,a≠1)是奇函数.
(1)求实数m的值;
(2)当x∈(n,a﹣2)时,函数f(x)的值域是(1,+∞),求实数a与n的值;
(3)设函数g(x)=﹣ax2+8(x﹣1)af(x)﹣5,a≥8时,存在最大实数t,使得x∈(1,t]时﹣5≤g(x)≤5恒成立,请写出t与a的关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】矩形ABCD中,AD=2,AB=4,E,F分别为边AB,AD的中点,将△ADE沿DE折起,点A,F折起后分别为点A′,F′,得到四棱锥A′﹣BCDE.给出下列几个结论:
①A′,B,C,F′四点共面;
②EF'∥平面A′BC;
③若平面A′DE⊥平面BCDE,则CE⊥A′D;
④四棱锥A′﹣BCDE体积的最大值为 ![]() .
.
其中正确的是(填上所有正确的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com