
【题目】团体购买公园门票,票价如下表:
购票人数 | 1~50 | 51~100 | 100以上 |
门票价格 | 13元/人 | 11元/人 | 9元/人 |
现某单位要组织其市场部和生产部的员工游览该公园,这两个部门人数分别为a和b![]() ,若按部门作为团体,选择两个不同的时间分别购票游览公园,则共需支付门票费为1290元;若两个部门合在一起作为一个团体,同一时间购票游览公园,则需支付门票费为990元,那么这两个部门的人数
,若按部门作为团体,选择两个不同的时间分别购票游览公园,则共需支付门票费为1290元;若两个部门合在一起作为一个团体,同一时间购票游览公园,则需支付门票费为990元,那么这两个部门的人数![]() ____;
____;![]() ____.
____.
【答案】70 40
【解析】
根据990不能被13整除,得两个部门人数之和:a+b≥51,然后结合门票价格和人数之间的关系,建立方程组进行求解即可.
∵990不能被13整除,∴两个部门人数之和:a+b≥51,
(1)若51≤a+b≤100,则11 (a+b)=990得:a+b=90,①
由共需支付门票费为1290元可知,11a+13b=1290 ②
解①②得:b=150,a=﹣60,不符合题意.
(2)若a+b≥100,则9 (a+b)=990,得 a+b=110 ③
由共需支付门票费为1290元可知,1≤a≤50,51≤b≤100,
得11a+13b=1290 ④,
解③④得:a=70人,b=40人,
故答案为:70,40.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且asin B=-bsin![]() .
.
(1)求A;
(2)若△ABC的面积S=![]() c2,求sin C的值.
c2,求sin C的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆过定点![]() ,在
,在![]() 轴截得的弦长为2.
轴截得的弦长为2.
(1)求动圆圆心的轨迹![]() 的方程;
的方程;
(2)若![]() 为轨迹
为轨迹![]() 上一动点,过点
上一动点,过点![]() 作圆
作圆![]() 的两条切线分别交
的两条切线分别交![]() 轴于
轴于![]() ,
,![]() 两点,求
两点,求![]() 面积的最小值,并求出此时点
面积的最小值,并求出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,梯形
中,梯形![]() 与平行四边形
与平行四边形![]() 所在平面互相垂直,
所在平面互相垂直, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
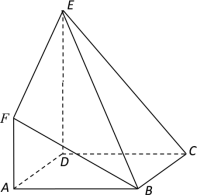
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)判断线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,求 出
?若存在,求 出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校在平面图为矩形的操场ABCD内进行体操表演,其中AB=40,BC=15,O为AB上一点,且BO=10,线段OC、OD、MN为表演队列所在位置(M、N分别在线段OD、OC上),△OCD内的点P为领队位置,且P到OC、OD的距离分别为![]() 、
、![]() ,记OM=d,我们知道当△OMN面积最小时观赏效果最好.
,记OM=d,我们知道当△OMN面积最小时观赏效果最好.
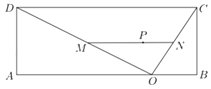
(1)当d为何值时,P为队列MN的中点;
(2)怎样安排M的位置才能使观赏效果最好?求出此时△OMN的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,
,![]() 为左焦点,
为左焦点,![]() 为上顶点,
为上顶点,![]() 为右顶点,若
为右顶点,若![]() ,抛物线
,抛物线![]() 的顶点在坐标原点,焦点为
的顶点在坐标原点,焦点为![]() .
.
(1)求![]() 的标准方程;
的标准方程;
(2)是否存在过![]() 点的直线,与
点的直线,与![]() 和
和![]() 交点分别是
交点分别是![]() 和
和![]() ,使得
,使得![]() ?如果存在,求出直线的方程;如果不存在,请说明理由.
?如果存在,求出直线的方程;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(I)求函数![]() 的对称轴方程;
的对称轴方程;
(II)将函数![]() 的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移
的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象.若
的图象.若![]() 分别是△ABC三个内角A,B,C的对边,a=2,c=4,且
分别是△ABC三个内角A,B,C的对边,a=2,c=4,且![]() ,求b的值.
,求b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com