
设函数 ,其中
,其中 .证明:当
.证明:当 时,函数
时,函数 没有极值点;当
没有极值点;当 时,函数
时,函数 有且只有一个极值点,并求出极值.
有且只有一个极值点,并求出极值.
当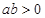 时,函数
时,函数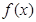 没有极值点;
没有极值点;
当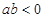 时,
时,
若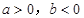 时,函数
时,函数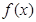 有且只有一个极小值点,极小值为
有且只有一个极小值点,极小值为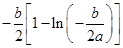 .
.
若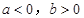 时,函数
时,函数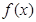 有且只有一个极大值点,极大值为
有且只有一个极大值点,极大值为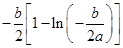 .
.
【解析】
试题分析:证明:因为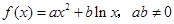 ,所以
,所以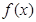 的定义域为
的定义域为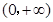 .
.
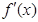
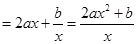 .
.
当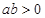 时,如果
时,如果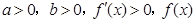 在
在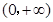 上单调递增;
上单调递增;
如果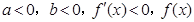 在
在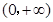 上单调递减.
上单调递减.
所以当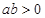 ,函数
,函数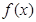 没有极值点.
没有极值点.
当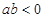 时,
时,
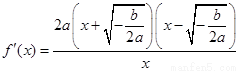
令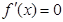 ,得
,得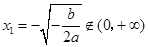 (舍去),
(舍去),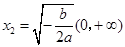 ,
,
当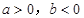 时,
时,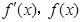 随
随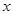 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
0 |
|
|
|
|
极小值 |
|
从上表可看出,
函数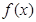 有且只有一个极小值点,极小值为
有且只有一个极小值点,极小值为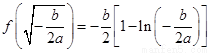 .
.
当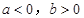 时,
时,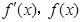 随
随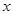 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
0 |
|
|
|
|
极大值 |
|
从上表可看出,
函数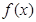 有且只有一个极大值点,极大值为
有且只有一个极大值点,极大值为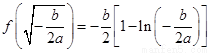 .
.
综上所述,当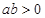 时,函数
时,函数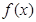 没有极值点;
没有极值点;
当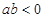 时,
时,
若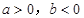 时,函数
时,函数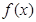 有且只有一个极小值点,极小值为
有且只有一个极小值点,极小值为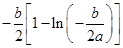 .
.
若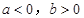 时,函数
时,函数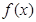 有且只有一个极大值点,极大值为
有且只有一个极大值点,极大值为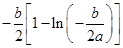 .
.
考点:函数的极值
点评:解决的关键是能对于含有参数的函数的导数的符号进行分类讨论,得到结论,属于中档题。


科目:高中数学 来源:2010-2011学年江西省南昌三中高三(上)10月月考数学试卷(文科)(解析版) 题型:解答题
 ,其中a为常数.
,其中a为常数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com