[题目]某车间为了规定工时定额.需确定加工零件所花费的时间.为此做了4次试验.得到的数据如下:零件的个数/个2345加工的时间/小时2.5344.5若加工时间与零件个数之间有较好的相关关系．(1)求加工时间与零件个数的线性回归方程．(2)试预报加工10个零件需要的时间．附录:参考公式:.. 题目和参考答案——青夏教育精英家教网—

【题目】某车间为了规定工时定额，需确定加工零件所花费的时间，为此做了4次试验，得到的数据如下：

零件的个数/个	2	3	4	5
加工的时间/小时	2.5	3	4	4.5

若加工时间与零件个数之间有较好的相关关系．

（1）求加工时间与零件个数的线性回归方程．

（2）试预报加工10个零件需要的时间．

附录：参考公式：，.

【答案】（1） y＝0.7x＋1.05.

（2） 8.05

【解析】

根据表中所给的数据，做出横标和纵标的平均数，得到样本中心点，求出对应的横标和纵标的积的和，求出横标的平方和，做出系数和的值，写出线性回归方程

将代入回归直线方程得出的值，即可预测加工个零件的时间，这是一个预报值。

（1）由表中数据，利用科学计算器得

xiyi＝52.5， x＝54，

因此，所求的线性回归方程为y＝0.7x＋1.05.

（2）将x＝10代入线性回归方程，得y＝0.7×10＋1.05＝8.05(小时)，即加工10个零件的预报时间为8.05小时．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

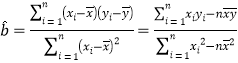科目：高中数学 来源： 题型：

【题目】判断下列两圆的位置关系.

(1)C1：x2＋y2－2x－3＝0，C2：x2＋y2－4x＋2y＋3＝0；___________

(2)C1：x2＋y2－2y＝0，C2：x2＋y2－2x－6＝0；___________

(3)C1：x2＋y2－4x－6y＋9＝0，C2：x2＋y2＋12x＋6y－19＝0；___________

(4)C1：x2＋y2＋2x－2y－2＝0，C2：x2＋y2－4x－6y－3＝0.___________

（5）x2＋y2＝9和x2＋y2－8x＋6y＋9＝0 ________________

（6）圆C1：x2＋y2－2x－6y－6＝0与圆C2：x2＋y2－4x＋2y＋4＝0______

（7）圆x2＋y2＋6x－7＝0和圆x2＋y2＋6y－27＝0 ____________

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某化工厂生产甲、乙两种混合肥料，需要A，B，C三种主要原料，生产1扯皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如表所示：

配料原料	A	B	C
甲	4	8	3
乙	5	5	10

现有A种原料200吨，B种原料360吨，C种原料300吨，在此基础上生产甲、乙两种肥料．已知生产1车皮甲种肥料，产生的利润为2万元；生产1车品乙种肥料，产生的利润为3万元、分别用x，y表示计划生产甲、乙两种肥料的车皮数．
（1）用x，y列出满足生产条件的数学关系式，并画出相应的平面区域；
（2）问分别生产甲、乙两种肥料，求出此最大利润．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】漳州市博物馆为了保护一件珍贵文物，需要在馆内一种透明又密封的长方体玻璃保护罩内充入保护液体.该博物馆需要支付的总费用由两部分组成：①罩内该种液体的体积比保护罩的容积少0.5立方米，且每立方米液体费用500元；②需支付一定的保险费用，且支付的保险费用与保护罩容积成反比，当容积为2立方米时，支付的保险费用为4000元.

（Ⅰ）求该博物馆支付总费用与保护罩容积之间的函数关系式；