
【题目】某地新建一家服装厂,从今年7月份开始投产,并且前4个月的产量分别为![]() 万件、
万件、![]() 万件、
万件、![]() 万件、
万件、![]() 万件.由于产品质量好,服装款式新颖,因此前几个月的产品销售情况良好.为了推销员在推销产品时接收订单不产生过多或过少的情况,需要估测以后几个月的产量,假如你是厂长,就月份x、产量y给出四种函数模型:
万件.由于产品质量好,服装款式新颖,因此前几个月的产品销售情况良好.为了推销员在推销产品时接收订单不产生过多或过少的情况,需要估测以后几个月的产量,假如你是厂长,就月份x、产量y给出四种函数模型:![]() ,
,![]() ,
,![]() ,
,![]() .你将利用零一种模型去估算以后几个月的产量?
.你将利用零一种模型去估算以后几个月的产量?
【答案】选用![]() 比较接近客观实际.
比较接近客观实际.
【解析】
由题意知![]() ,
,![]() ,
,![]() ,
,![]() ,根据其中某些点确定函数模型,再求解其他点的估计值,计算误差值,取误差值最小以及有上升趋势的函数模型,即可.
,根据其中某些点确定函数模型,再求解其他点的估计值,计算误差值,取误差值最小以及有上升趋势的函数模型,即可.
解:由题意知![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)对于一次函数模型![]() ,将B,C两点的坐标分別代入,得
,将B,C两点的坐标分別代入,得![]() 解得
解得![]()
![]() .
.
将点A的横坐标代入,得![]() ,与实际误差为0.1;将点D的横标代入,得
,与实际误差为0.1;将点D的横标代入,得![]() ,与实际误差为0.03.
,与实际误差为0.03.
(2)对于二次函数模型![]() ,将A,B,C三点的坐标分别代入,得
,将A,B,C三点的坐标分别代入,得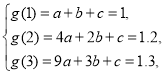 解得
解得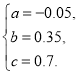
![]() .
.
将点D的横坐标代入,得![]() ,与实际误差为0.07.
,与实际误差为0.07.
(3)对于幂函数模型![]() ,将A,B两点的坐标分别代入,得
,将A,B两点的坐标分别代入,得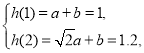 解得
解得![]()
![]() .
.
将C,D两点的横坐标分别代入,得![]() ,与实际误差为0.05;
,与实际误差为0.05;
![]() ,与实际误差为0.11.
,与实际误差为0.11.
(4)对于指数型函数模型![]() ,将A,B,C三点的坐标分别代入,得
,将A,B,C三点的坐标分别代入,得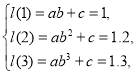 解得
解得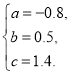
![]() .
.
将点D的横坐标代入,得![]() ,与实际误差为0.02.
,与实际误差为0.02.
比较上述四个模拟函数的优劣,既要考虑误差最小,又要考虑生产的实际问题,比如增产的趋势和可能性,可以认为![]() 最佳.一是误差最小,二是由于新建厂,开始随着工人技术管理效益逐渐提高,一段时间内产量明显上升,但到一定时期后,设备不更新,而么产量必然要趋于稳定,而
最佳.一是误差最小,二是由于新建厂,开始随着工人技术管理效益逐渐提高,一段时间内产量明显上升,但到一定时期后,设备不更新,而么产量必然要趋于稳定,而![]() 恰好反映了这种趋势,因此选用
恰好反映了这种趋势,因此选用![]() 比较接近客观实际.
比较接近客观实际.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)=x2+(a+1)x+a2(a∈R),若f(x)能表示成一个奇函数g(x)和一个偶函数h(x)的和.
(1)求g(x)和h(x)的解析式;
(2)若f(x)和g(x)在区间(-∞,(a+1)2]上都是减函数,求f(1)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一个半圆形湖面景点的平面示意图.已知![]() 为直径,且
为直径,且![]() km,
km,![]() 为圆心,
为圆心,![]() 为圆周上靠近
为圆周上靠近![]() 的一点,
的一点,![]() 为圆周上靠近
为圆周上靠近![]() 的一点,且
的一点,且![]() ∥
∥![]() .现在准备从
.现在准备从![]() 经过
经过![]() 到
到![]() 建造一条观光路线,其中
建造一条观光路线,其中![]() 到
到![]() 是圆弧
是圆弧![]() ,
,![]() 到
到![]() 是线段
是线段![]() .设
.设![]() ,观光路线总长为
,观光路线总长为![]() .
.

(1)求![]() 关于
关于![]() 的函数解析式,并指出该函数的定义域;
的函数解析式,并指出该函数的定义域;
(2)求观光路线总长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ,(
,( ![]() 为参数),
为参数),![]() 为曲线
为曲线![]() 上的动点,动点
上的动点,动点![]() 满足
满足![]() (
(![]() 且
且![]() ),
),![]() 点的轨迹为曲线
点的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程,并说明
的方程,并说明![]() 是什么曲线;
是什么曲线;
(2)在以坐标原点为极点,以![]() 轴的正半轴为极轴的极坐标系中,
轴的正半轴为极轴的极坐标系中, ![]() 点的极坐标为
点的极坐标为![]() ,射线
,射线![]() 与
与![]() 的异于极点的交点为
的异于极点的交点为![]() ,已知
,已知![]() 面积的最大值为
面积的最大值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲商店某种商品4月份(30天,4月1日为第一天)的销售价格P(元)与时间t(天)的函数关系如图所示(1),该商品日销售量Q(件)与时间t(天)的函数关系如图(2)所示.
(1) (2)
(2)
(1)写出图(1)表示的销售价格与时间的函数关系式![]() ,写出图(2)表示的日销售量与时间的函数关系式
,写出图(2)表示的日销售量与时间的函数关系式![]() 及日销售金额M(元)与时间的函数关系式
及日销售金额M(元)与时间的函数关系式![]() .
.
(2)乙商店销售同一种商品,在4月份采用另一种销售策略,日销售金额N(元)与时间t(天)之间的函数关系式为![]() ,试比较4月份每天两商店销售金额的大小关系。
,试比较4月份每天两商店销售金额的大小关系。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出如下四个命题:①若“![]() 且
且![]() ”为假命题,则
”为假命题,则![]() 均为假命题;②命题“若
均为假命题;②命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”; ③“
”; ③“![]() ,则
,则![]() ”的否定是“
”的否定是“![]() ,则
,则![]() ”;④在
”;④在![]() 中,“
中,“![]() ”是“
”是“![]() ”的充要条件.其中正确的命题的个数是( )
”的充要条件.其中正确的命题的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各题中,哪些p是q的充要条件?
(1)p:四边形是正方形,q:四边形的对角线互相垂直且平分;
(2)p:两个三角形相似,q:两个三角形三边成比例;
(3)![]() ,
,![]() ,
,![]() ;
;
(4)![]() 是一元二次方程
是一元二次方程![]() 的一个根,
的一个根,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在古代三国时期吴国的数学家赵爽创制了一幅“赵爽弦图”,由四个全等的直角三角形围成一个大正方形,中间空出一个小正方形(如图阴影部分)。若直角三角形中较小的锐角为a。现向大正方形区城内随机投掷一枚飞镖,要使飞镖落在小正方形内的概率为![]() ,则
,则![]() _____________。
_____________。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com