
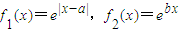 .
.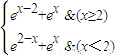 ,再对x进行分类讨论:①当x≥2时;②当x<2时;利用导数工具研究其单调性即得;
,再对x进行分类讨论:①当x≥2时;②当x<2时;利用导数工具研究其单调性即得;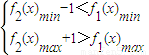 .再对字母b分类讨论:①当b≥0时,②当b<0时.即可求得a的取值范围.
.再对字母b分类讨论:①当b≥0时,②当b<0时.即可求得a的取值范围.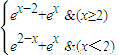 ,…(5分)
,…(5分)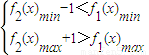 …(10分)
…(10分)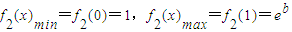
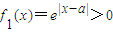 ,
,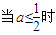 ,
,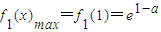 ,
,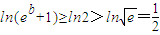
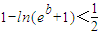
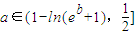
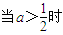
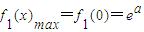
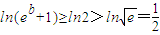
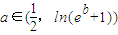
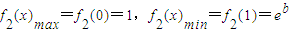
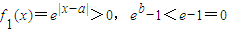
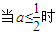
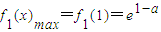
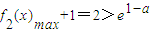
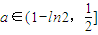 ,
, ,
,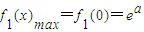 .
.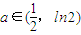


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源:2011-2012学年安徽省省城名校高三第一次联考数学试卷(理科)(解析版) 题型:解答题
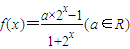 .
.查看答案和解析>>
科目:高中数学 来源:宁夏回族自治区月考题 题型:解答题
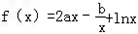 .
. 处取和极值,
处取和极值,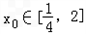 ,使得不等式f(
,使得不等式f(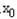 )-c≤0成立,求c的最小值;
)-c≤0成立,求c的最小值;查看答案和解析>>
科目:高中数学 来源:2010年高考数学预测试卷(押题卷1)(解析版) 题型:解答题
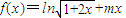 .
.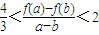 .
.查看答案和解析>>
科目:高中数学 来源:2010年四川省攀枝花市高考数学三模试卷(理科)(解析版) 题型:解答题
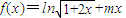 .
.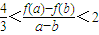 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com