Question

（08年哈九中） 已知斜三棱柱的各棱长均为2， 侧棱与底面所成角为，

且侧面底面.

（1）证明：点在平面上的射影为的中点；

（2）求二面角的大小 ；

（3）求点到平面的距离.

 

 

Answer 1

解析:（1）证明：过B₁点作B₁O⊥BA。∵侧面ABB₁A₁⊥底面ABC

∴A₁O⊥面ABC ∴∠B₁BA是侧面BB₁与底面ABC倾斜角

∴∠B₁BO=  在Rt△B₁OB中，BB₁=2，∴BO=BB₁=1

又∵BB₁=AB，∴BO=AB ∴O是AB的中点。

即点B₁在平面ABC上的射影O为AB的中点                                       

   （2）连接AB₁过点O作OM⊥AB₁，连线CM，OC，

∵OC⊥AB，平面ABC⊥平面AA₁BB₁ ∴OC⊥平面AABB。

∴OM是斜线CM在平面AA₁B₁B的射影 ∵OM⊥AB₁

∴AB₁⊥CM  ∴∠OMC是二面角C―AB₁―B的平面角

在Rt△OCM中，OC=，OM=

∴∠OMC=cosC+sin2

∴二面角C―AB₁―B的大小为                                              

   （3）过点O作ON⊥CM，∵AB₁⊥平面OCM，∴AB₁⊥ON

∴ON⊥平面AB₁C。∴ON是O点到平面AB₁C的距离

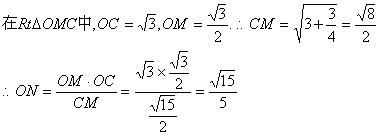
连接BC₁与B₁C相交于点H，则H是BC₁的中点

∴B与C₁到平面ACB₁的相导。

又∵O是AB的中点 ∴B到平面AB₁C的距离

是O到平面AB₁C距离的2倍

    是G到平面AB₁C距离为