
分析 若不等式ln(1+x)≥$\frac{ax}{1+x}$恒成立,f(x)=(1+x)ln(1+x)≥ax恒成立,利用导数法分析函数的图象和性质,数形结合可得答案.
解答 解:若不等式ln(1+x)≥$\frac{ax}{1+x}$恒成立,
f(x)=(1+x)ln(1+x)≥ax恒成立,
∵f′(x)=ln(1+x)+1=0时,x=$\frac{1}{e}$-1,
当x∈(-1,$\frac{1}{e}$-1)时,f′(x)<0,函数为减函数,
当x∈($\frac{1}{e}$-1,+∞)时,f′(x)>0,函数为增函数,
故f(x)的图象如下图所示: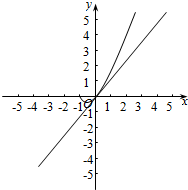
又由直线y=ax的图象过原点,f′(0)=1
故当a=1时,f(x)=(1+x)ln(1+x)≥ax恒成立,
即不等式ln(1+x)≥$\frac{ax}{1+x}$恒成立.
点评 本题考查的知识点是恒成立问题,数形结合思想,导数法分析函数的单调性,难度中档.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\sqrt{{x}^{2}}$,g(x)=($\sqrt{x}$)2 | B. | f(x)=(x-1)0,g(x)=1 | ||
| C. | f(x)=$\frac{{x}^{2}-1}{x-1}$,g(x)=x+1 | D. | f(x)=$\sqrt{{x}^{2}}$,g(t)=|t| |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知函数f(x)=2sin(ωx+φ)其中x∈R,ω>0,-π<φ<π)的部分图象如图所示,则函数f(x)的解析式是$f(x)=2sin(2x+\frac{2π}{3})$.
已知函数f(x)=2sin(ωx+φ)其中x∈R,ω>0,-π<φ<π)的部分图象如图所示,则函数f(x)的解析式是$f(x)=2sin(2x+\frac{2π}{3})$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1-a)a>(1+a)a | B. | log1-a(1+a)<0 | C. | (1-a)1+a>1 | D. | ${(1-a)}^{\frac{1}{a}}$>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com