Question

 

（文）一个口袋装有大小相同的2个白球和3个黑球，从中摸出2个球.

求：（Ⅰ）两个球恰好颜色相同的概率；

（Ⅱ）两个球恰好颜色不同的概率.    

（理）已知10件产品中有3件是次品.

    （Ⅰ）任意取出3件产品作检验，求其中至少有1件是次品的概率；

    （Ⅱ）为了保证使3件次品全部检验出的概率超过0.6，最少应抽取几件产品作检验？

 

 

 

 

 

 

Answer 1

【答案】

 （文）解：（Ⅰ）两球恰好颜色相同的概率为:P₁ =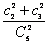==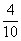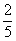(或0.4)………6分

2n

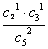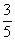（Ⅱ）两球恰好颜色不同的概率为：P₂ ===0.6………………………12分

（理）解：（Ⅰ）任意取出3件产品作检验，全部是正品的概率为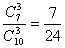……3分

至少有一件是次品的概率为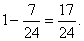……………………6分

（Ⅱ）设抽取n件产品作检验，则3件次品全部检验出的概率为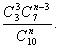…8分

由

整理得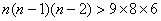：，……………………10分   

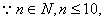   ∴当n=9或n=10时上式成立.…………11分

答：任意取出3件产品作检验，其中至少有1件是次品的概率为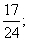为了保证使3件次品全部检验出的概率超过0.6，最少应抽取9件产品作检验.………………12分