
【题目】已知函数f(x)=lg(ax-bx),(a>1>b>0).
(1)求f(x)的定义域;
(2)若f(x)在(1,+∞)上递增且恒取正值,求a,b满足的关系式.
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:
【题目】如图,已知![]() 是半圆
是半圆![]() 的直径,
的直径,![]() ,
,![]() 是将半圆圆周四等分的三个分点.
是将半圆圆周四等分的三个分点.

(1)从![]() 这5个点中任取3个点,求这3个点组成直角三角形的概率;
这5个点中任取3个点,求这3个点组成直角三角形的概率;
(2)在半圆内任取一点![]() ,求
,求![]() 的面积大于
的面积大于![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的左焦点F为圆
的左焦点F为圆![]() 的圆心,且椭圆C上的点到点F的距离最小值为
的圆心,且椭圆C上的点到点F的距离最小值为![]() 。
。
(I)求椭圆C的方程;
(II)已知经过点F的动直线![]() 与椭圆C交于不同的两点A、B,点M坐标为(
与椭圆C交于不同的两点A、B,点M坐标为(![]() ),证明:
),证明: ![]() 为定值。
为定值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017届陕西省西安市铁一中学高三上学期第五次模拟考试数学(文)】已知向量![]() ,
,![]() ,且函数
,且函数![]() .
.
(Ⅰ)当函数在![]() 上的最大值为3时,求
上的最大值为3时,求的值;
(Ⅱ)在(Ⅰ)的条件下,若对任意的![]() ,函数
,函数,![]() 的图像与直线
的图像与直线有且仅有两个不同的交点,试确定的值.并求函数在上的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(-x2+x-1)ex,其中e是自然对数的底数.
(1)求曲线f(x)在点(1,f(1))处的切线;
(2)若方程f(x)=![]() x3+
x3+![]() x2+m有3个不同的根,求实数m的取值范围.
x2+m有3个不同的根,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列三个结论:
①小王任意买1张电影票,座号是3的倍数的可能性比座号是5的倍数的可能性大;
②高一(1)班有女生22人,男生23人,从中任找1人,则找出的女生可能性大于找出男生的可能性;
③掷1枚质地均匀的硬币,正面朝上的可能性与反面朝上的可能性相同.
其中正确结论的序号为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017兰州高考模拟】.在多面体ABCDEF中,底面ABCD是梯形,四边形ADEF是正方形,AB∥DC,AB=AD=1,CD=2,AC=EC=![]() 。
。
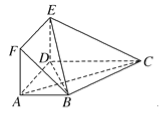
(1)求证:平面EBC⊥平面EBD;
(2)设M为线段EC上一点,且3EM=EC,试问在线段BC上是否存在一点T,使得MT∥平面BDE,若存在,试指出点T的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“开门大吉”是中央电视台推出的娱乐节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌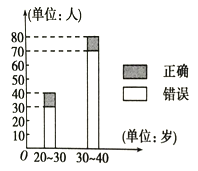
的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示.
(1) 完成下列2×2列联表(见答题纸);
(2)判断是否有90%的把握认为猜对歌曲名称与否和年龄有关;说明你的理由.(下面的临界值表供参考)
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
(参考公式: 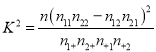 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ax3-bx2+(2-b)x+1在x=x1处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2.
ax3-bx2+(2-b)x+1在x=x1处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2.
(1)证明:a>0;
(2)若z=a+2b,求z的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com