【答案】
分析:解:(1)由f(x)=
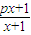
结合b
n=f
-1(n)若对于任意n∈N
*都有b
n=a
n求解,
(2)由正整数c
n的前n项和
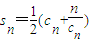
则由通项与前n项和之间的关系求解,要注意分类讨论;
(3)在(1)和(2)的条件下,d
1=2,∴D
1=2,则n≥2时,
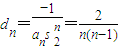
,由D
n是数列d
n的前n项和有D
n=
1+d
2+…+d
n用裂项相消法求解
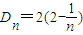
,再由D
n>log
a(1-2a)恒成立,即log
a(1-2a)小于D
n的最小值,只要求得D
n的最小值即可.
解答:解:(1)由题意得
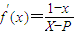
∵
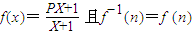
∴P=-1∴
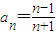
(2)∵正整数c
n的前n项和
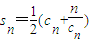
∴
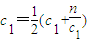
解之得∴c
1=1,s
1=1
当n≥2时,c
n=s
n-s
n-1∴
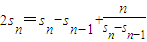
∴
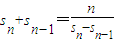
s
n2-s
n-12=n
∴s
n-12-s
n-22=n-1
s
n-22-s
n-22=n-2
s
22-s
12=2
以上各式累加,得∴
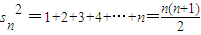
,
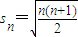
(3)在(1)和(2)的条件下,d
1=2∴D
1=2
当n≥2时,设
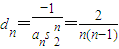
,由D
n是数列d
n的前n项和
有D
n=
1+d
2+…+d
n=
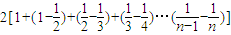
=
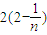
综上
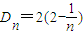
因为D
n>log
a(1-2a)恒成立,所以log
a(1-2a)小于D
n的最小值,
显然D
n的最小值在n=1时取得,即[D
n]
min=2
∴log
a(1-2a)<2
∴a满足的条件是
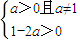
,∴log
a(1-2a)<2
解得
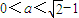 点评:
点评:本题一道新定义题,考查了反函数的求法,数列通项与前n项和间的关系以及累加法求通项和裂项相消法求前n项和等知识和方法,综合性较强.

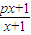 ,若由函数f(x)确定的数列{an}的自反数列为{bn},求an;
,若由函数f(x)确定的数列{an}的自反数列为{bn},求an; (cn+
(cn+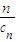 ).写出Sn表达式,并证明你的结论;
).写出Sn表达式,并证明你的结论;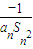 ,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.
,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.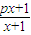 结合bn=f-1(n)若对于任意n∈N*都有bn=an求解,
结合bn=f-1(n)若对于任意n∈N*都有bn=an求解,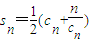 则由通项与前n项和之间的关系求解,要注意分类讨论;
则由通项与前n项和之间的关系求解,要注意分类讨论;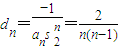 ,由Dn是数列dn的前n项和有Dn=1+d2+…+dn用裂项相消法求解
,由Dn是数列dn的前n项和有Dn=1+d2+…+dn用裂项相消法求解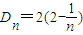 ,再由Dn>loga(1-2a)恒成立,即loga(1-2a)小于Dn的最小值,只要求得Dn的最小值即可.
,再由Dn>loga(1-2a)恒成立,即loga(1-2a)小于Dn的最小值,只要求得Dn的最小值即可.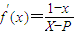
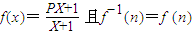
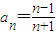
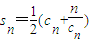
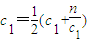
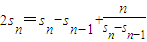
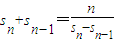
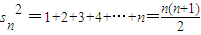 ,
,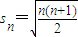
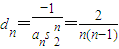 ,由Dn是数列dn的前n项和
,由Dn是数列dn的前n项和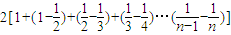
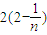
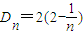
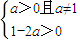 ,∴loga(1-2a)<2
,∴loga(1-2a)<2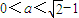


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案