
【题目】己知函数![]() .(
.(![]() 是常数,且(
是常数,且(![]() )
)
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 在
在![]() 处取得极值时,若关于
处取得极值时,若关于![]() 的方程
的方程![]() 在
在![]() 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)求证:当![]() 时
时![]() .
.
【答案】(Ⅰ)减区间为![]() ,增区间为.
,增区间为.![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)见解析.
;(Ⅲ)见解析.
【解析】分析:(Ⅰ)先对函数![]() 求导,再分别解
求导,再分别解![]() 与
与![]() ,即可得函数
,即可得函数![]() 的单调区间;(Ⅱ)根据
的单调区间;(Ⅱ)根据![]() 在
在![]() 处取得极值,可得
处取得极值,可得![]() ,再设
,再设![]() ,利用导数研究函数
,利用导数研究函数![]() 的单调性,根据关于
的单调性,根据关于![]() 的方程
的方程![]() 在
在![]() 上恰有两个不相等的实数根,可得
上恰有两个不相等的实数根,可得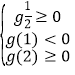 ,解不等式即可得出实数
,解不等式即可得出实数![]() 的取值范围;(Ⅲ)根据(Ⅰ)和(Ⅱ)可知当
的取值范围;(Ⅲ)根据(Ⅰ)和(Ⅱ)可知当![]() 时,
时,![]() 即
即![]() ,令
,令![]() ,对
,对![]() 进行放缩,即可证明.
进行放缩,即可证明.
详解:(Ⅰ)由已知比函数![]() 的定义域为
的定义域为![]() ,
,
由![]() 得
得![]() ,由
,由![]() ,得
,得![]() .
.
所以函数![]() 的减区间为
的减区间为![]() ,增区间为.
,增区间为.![]() .
.
(Ⅱ)由题意,得![]() .
.
∴![]()
∴![]()
∴![]() ,即
,即![]() .
.
∴![]() ,
,
设![]() ,则
,则![]() .
.
当![]() 变化时,
变化时,![]() 的变化情况如下表:
的变化情况如下表:
|
|
| 1 |
| 2 |
| 0 | - | 0 | + | |
|
|
|
|
|
|
∵方程![]() 在
在![]() 上恰有两个不相等的实数根
上恰有两个不相等的实数根
∴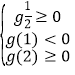
∴
∴![]() 即
即![]() .
.
(Ⅲ)由(Ⅰ)和(Ⅱ)可知当![]() 时,
时,![]() 即
即![]() ,
,
∴当![]() 时,
时,![]() ,
,
令![]() 时,
时,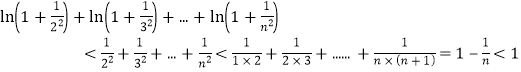 ,即
,即![]() .
.
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】记焦点在同一条轴上且离心率相同的椭圆为“相似椭圆”.已知椭圆![]() ,以椭圆
,以椭圆![]() 的焦点为顶点作相似椭圆
的焦点为顶点作相似椭圆![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
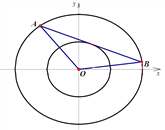
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且与椭圆
两点,且与椭圆![]() 仅有一个公共点,试判断
仅有一个公共点,试判断![]() 的面积是否为定值(
的面积是否为定值(![]() 为坐标原点)?若是,求出该定值;若不是,请说明理由.
为坐标原点)?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人去某地务工,其工作受天气影响,雨天不能出工,晴天才能出工.其计酬方式有两种,方式一:雨天没收入,晴天出工每天![]() 元;方式而:雨天每天
元;方式而:雨天每天![]() 元,晴天出工每天
元,晴天出工每天![]() 元;三人要选择其中一种计酬方式,并打算在下个月(
元;三人要选择其中一种计酬方式,并打算在下个月(![]() 天)内的晴天都出工,为此三人作了一些调查,甲以去年此月的下雨天数(
天)内的晴天都出工,为此三人作了一些调查,甲以去年此月的下雨天数(![]() 天)为依据作出选择;乙和丙在分析了当地近
天)为依据作出选择;乙和丙在分析了当地近![]() 年此月的下雨天数(
年此月的下雨天数(![]() )的频数分布表(见下表)后,乙以频率最大的
)的频数分布表(见下表)后,乙以频率最大的![]() 值为依据作出选择,丙以
值为依据作出选择,丙以![]() 的平均值为依据作出选择.
的平均值为依据作出选择.
| 8 | 9 | 10 | 11 | 12 | 13 |
频数 | 3 | 1 | 2 | 0 | 2 | 1 |
(Ⅰ)试判断甲、乙、丙选择的计酬方式,并说明理由;
(Ⅱ)根据统计范围的大小,你觉得三人中谁的依据更有指导意义?
(Ⅲ)以频率作为概率,求未来三年中恰有两年,此月下雨不超过![]() 天的概率.
天的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台“挑战主持人”节目的挑战者闯第一关需要回答三个问题,其中前两个问题回答正确各得![]() 分,回答不正确得
分,回答不正确得![]() 分,第三个问题回答正确得
分,第三个问题回答正确得![]() 分,回答不正确得
分,回答不正确得![]() 分.如果一个挑战者回答前两个问题正确的概率都是
分.如果一个挑战者回答前两个问题正确的概率都是![]() ,回答第三个问题正确的概率为
,回答第三个问题正确的概率为![]() ,且各题回答正确与否相互之间没有影响.若这位挑战者回答这三个问题总分不低于
,且各题回答正确与否相互之间没有影响.若这位挑战者回答这三个问题总分不低于![]() 分就算闯关成功.
分就算闯关成功.
(Ⅰ)求至少回答对一个问题的概率;
(Ⅱ)求这位挑战者回答这三个问题的总得分X的分布列;
(Ⅲ)求这位挑战者闯关成功的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com