
【题目】某市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是 ![]() ,样本数据分组为
,样本数据分组为![]() ,
,![]() .
.
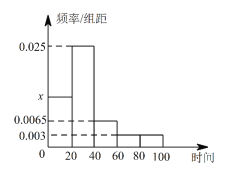
(Ⅰ)求直方图中![]() 的值;
的值;
(Ⅱ)如果年上缴税收不少于![]() 万元的企业可申请政策优惠,若共抽取企业
万元的企业可申请政策优惠,若共抽取企业![]() 个,试估计有多少企业可以申请政策优惠;
个,试估计有多少企业可以申请政策优惠;
(Ⅲ)从企业中任选![]() 个,这
个,这![]() 个企业年上缴税收少于
个企业年上缴税收少于![]() 万元的个数记为
万元的个数记为 ![]() ,求
,求![]() 的分布列和数学期望.(以直方图中的频率作为概率)
的分布列和数学期望.(以直方图中的频率作为概率)
科目:高中数学 来源: 题型:
【题目】贵阳河滨公园是市民休闲游玩的重要场所,某校社团针对“公园环境评价”随机对![]() 位市民进行问卷调查打分(满分100分)得茎叶图如下:
位市民进行问卷调查打分(满分100分)得茎叶图如下:

(1)写出女性打分的中位数和众数;
(2)从打分在![]() 分以下(不含
分以下(不含![]() 分)的市民中随机请
分)的市民中随机请![]() 人进一步提建议,求这
人进一步提建议,求这![]() 人都是男性市民的概率.
人都是男性市民的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下命题:
(1)若![]() :
:![]() ;
;![]() :
:![]() ,则
,则![]() 为真,
为真,![]() 为假,
为假,![]() 为真
为真
(2)“![]() ”是“曲线
”是“曲线![]() 表示椭圆”的充要条件
表示椭圆”的充要条件
(3)命题“若![]() ,则
,则![]() ”的否命题为:“若
”的否命题为:“若![]() ,则
,则![]() ”
”
(4)如果将一组数据中的每一个数都加上同一个非零常数,那么这组数据的平均数和方差都改变;
则正确命题有( )个
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学用简单随机抽样方法抽取了100名同学,对其社会实践次数进行调查,结果如下:
|
|
|
|
|
|
|
男同学人数 | 7 | 15 | 11 | 12 | 2 | 1 |
女同学人数 | 5 | 13 | 20 | 9 | 3 | 2 |
若将社会实践次数不低于12次的学生称为“社会实践标兵”.
(Ⅰ)将频率视为概率,估计该校1600名学生中“社会实践标兵”有多少人?
(Ⅱ)从已抽取的8名“社会实践标兵”中随机抽取4位同学参加社会实践表彰活动.
(i)设![]() 为事件“抽取的4位同学中既有男同学又有女同学”,求事件
为事件“抽取的4位同学中既有男同学又有女同学”,求事件![]() 发生的概率;
发生的概率;
(ii)用![]() 表示抽取的“社会实践标兵”中男生的人数,求随机变量
表示抽取的“社会实践标兵”中男生的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 分别为双曲线
分别为双曲线![]() 的左、右焦点。若在双曲线右支上存在点
的左、右焦点。若在双曲线右支上存在点![]() ,满足
,满足![]() ,且
,且![]() 到直线
到直线![]() 的距离等于双曲线的实轴长,则该双曲线的渐近线与抛物线
的距离等于双曲线的实轴长,则该双曲线的渐近线与抛物线![]() 的准线围成三角形的面积为( )
的准线围成三角形的面积为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,
,![]() 两点,
两点,![]() 是该抛物线上位于第一象限内的点.
是该抛物线上位于第一象限内的点.

(Ⅰ) 记直线![]() 的斜率分别为
的斜率分别为![]() ,求证:
,求证:![]() 为定值;
为定值;
(Ⅱ)过点![]() 作
作![]() ,垂足为
,垂足为![]() .若
.若![]() 关于
关于![]() 轴的对称点恰好在直线
轴的对称点恰好在直线![]() 上,求
上,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线![]() :
:![]() ,以极点
,以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴的正半轴建立平面直角坐标系,过点
轴的正半轴建立平面直角坐标系,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为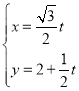 (
(![]() 为参数),点
为参数),点![]() 在直线
在直线![]() 上,且
上,且![]() .
.
(Ⅰ)求点![]() 的极坐标;
的极坐标;
(Ⅱ)若点![]() 是曲线
是曲线![]() 上一动点,求点
上一动点,求点![]() 到直线
到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角梯形PBCD中,∠D=∠C![]() ,BC=CD=2,PD=4,A为PD的中点,如图1,将△PAB沿AB折到△SAB的位置,使SB⊥BC,点E在SD上,如图2.
,BC=CD=2,PD=4,A为PD的中点,如图1,将△PAB沿AB折到△SAB的位置,使SB⊥BC,点E在SD上,如图2.
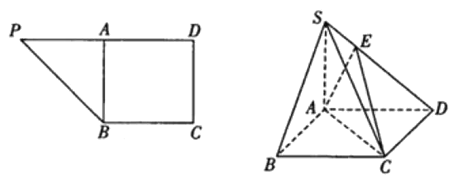
(1)求证:SA⊥平面ABCD;
(2)若E为SD中点,求D点到面EAC的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com