
【题目】在某地区某高传染性病毒流行期间,为了建立指标显示校情已受控制,以便向该地区居众显示可以过正常生活,有公共卫生专家建议的指标是“连续![]() 天每天新增感染人数不超过
天每天新增感染人数不超过![]() 人”,根据连续
人”,根据连续![]() 天的新增病例数计算,下列各项选项中,一定符合上述指标的是( )
天的新增病例数计算,下列各项选项中,一定符合上述指标的是( )
①平均数![]() ;
;
②标准差![]() ;
;
③平均数![]() ;且标准差
;且标准差![]() ;
;
④平均数![]() ;且极差小于或等于
;且极差小于或等于![]() ;
;
⑤众数等于![]() 且极差小于或等于
且极差小于或等于![]() .
.
A.①②B.③④C.③④⑤D.④⑤
【答案】D
【解析】
通过举反例说明①②③不符合条件,④⑤通过平均数和标准差的统计意义,找出符合要求的选项.
对①②③举反例判断,对于④分情况讨论,对于⑤结合题意判断即可.
解:①错,举反例:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其平均数
,其平均数![]() ,但不符合题意,
,但不符合题意,
②错,举反例:6,6,6,6,6,6,6,其标准差![]() ,但不符合题意,
,但不符合题意,
③错,举反例:0,0,0,0,0,1,6,平均数![]() ,且标准差
,且标准差![]() ;但不符合题意,
;但不符合题意,
④对,若极差小于2,显然符合条件,
若极差小于等于2,有可能(1)0,1,2;(2)1,2,3;(3)2,3,4;(4)3,4,5;(5)4,5,6.
在平均数![]() 的条件下,只有(1)(2)(3)成立,符合条件.
的条件下,只有(1)(2)(3)成立,符合条件.
⑤对,在众数等于1且极差小于等于4时,最大数不超过5,符合条件.
故选:D.


科目:高中数学 来源: 题型:
【题目】(本小题满分10分)[选修4-5:不等式选讲]
已知函数![]() =|x-a|+
=|x-a|+![]() (a≠0)
(a≠0)
(1)若不等式![]() -
-![]() ≤1恒成立,求实数m的最大值;
≤1恒成立,求实数m的最大值;
(2)当a<![]() 时,函数g(x)=
时,函数g(x)=![]() +|2x-1|有零点,求实数a的取值范围
+|2x-1|有零点,求实数a的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线
中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为![]()
![]() 为参数,曲线
为参数,曲线![]() 上的点
上的点![]() 的极坐标分别为
的极坐标分别为![]() .
.
(1)过O作线段![]() 的垂线,垂足为H,求点H的轨迹
的垂线,垂足为H,求点H的轨迹![]() 的直角坐标方程;
的直角坐标方程;
(2)求![]() 两点间的距离的取值范围.
两点间的距离的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下命题:
(1)已知回归直线方程为![]() ,样本点的中心为
,样本点的中心为![]() ,则
,则![]() ;
;
(2)已知![]() ,
,![]() 与
与![]() 的夹角为钝角,则
的夹角为钝角,则![]() 是
是![]() 的充要条件;
的充要条件;
(3)函数![]() 图象关于点
图象关于点![]() 对称且在
对称且在![]() 上单调递增;
上单调递增;
(4)命题“存在![]() ”的否定是“对于任意
”的否定是“对于任意![]() ”;
”;
(5)设函数![]() ,若函数
,若函数![]() 恰有三个零点,则实数m的取值范围为
恰有三个零点,则实数m的取值范围为![]() .
.
其中不正确的命题序号为______________ .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·石家庄一模)祖暅是南北朝时期的伟大数学家,5世纪末提出体积计算原理,即祖暅原理:“幂势既同,则积不容异”.意思是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任何一个平面所截,如果截面面积都相等,那么这两个几何体的体积一定相等.现有以下四个几何体:图①是从圆柱中挖去一个圆锥所得的几何体,图②、图③、图④分别是圆锥、圆台和半球,则满足祖暅原理的两个几何体为( )
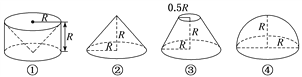
A. ①② B. ①③
C. ②④ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 过原点且倾斜角为
过原点且倾斜角为![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立坐标系,曲线
轴正半轴为极轴建立坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .在平面直角坐标系
.在平面直角坐标系![]() 中,曲线
中,曲线![]() 与曲线
与曲线![]() 关于直线
关于直线![]() 对称.
对称.
(Ⅰ)求曲线![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)若直线![]() 过原点且倾斜角为
过原点且倾斜角为![]() ,设直线
,设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,直线
两点,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,当
两点,当![]() 变化时,求
变化时,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过点
经过点![]() 且与直线
且与直线![]() 相切,圆心
相切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]() ,点
,点![]()
![]() 为曲线
为曲线![]() 上一点.
上一点.
(1)求![]() 的值及曲线
的值及曲线![]() 的方程;
的方程;
(2)若![]() 为曲线
为曲线![]() 上异于
上异于![]() 的两点,且
的两点,且![]() .记点
.记点![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() ,判断
,判断![]() 是否为定值,若是,请求出该定值;若不是,请说明理由.
是否为定值,若是,请求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生活超市有一专柜预代理销售甲乙两家公司的一种可相互替代的日常生活用品.经过一段时间分别单独试销甲乙两家公司的商品,从销售数据中随机各抽取50天,统计每日的销售数量,得到如下的频数分布条形图.甲乙两家公司给该超市的日利润方案为:甲公司给超市每天基本费用为90元,另外每销售一件提成1元;乙公司给超市每天的基本费用为130元,每日销售数量不超过83件没有提成,超过83件的部分每件提成10元.
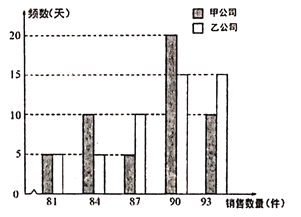
(Ⅰ)求乙公司给超市的日利润![]() (单位:元)与日销售数量
(单位:元)与日销售数量![]() 的函数关系;
的函数关系;
(Ⅱ)若将频率视为概率,回答下列问题:
(1)求甲公司产品销售数量不超过87件的概率;
(2)如果仅从日均利润的角度考虑,请你利用所学过的统计学知识为超市作出抉择,选择哪家公司的产品进行销售?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com