
(08年杨浦区测试)设抛物线![]() 的焦点为
的焦点为![]() ,经过点
,经过点![]() 的直线交抛物线于
的直线交抛物线于![]() 、
、![]() 两点,且
两点,且![]() 、
、![]() 两点坐标分别为
两点坐标分别为![]() ,
,![]() 是抛物线的准线上的一点,
是抛物线的准线上的一点,![]() 是坐标原点.若直线
是坐标原点.若直线![]() 、
、![]() 、
、![]() 的斜率分别记为:
的斜率分别记为:![]() 、
、![]() 、
、![]() ,(如图)
,(如图)
(1)若![]() ,求抛物线的方程.
,求抛物线的方程.
(2)当![]() 时,求
时,求![]() 的值.
的值.
(3)如果取![]() ,
,![]() 时,
时,
(文科考生做)判定![]() 和
和![]() 的值大小关系.并说明理由.
的值大小关系.并说明理由.
(理科考生做)判定![]() 和
和![]() 的值大小关系.并说明理由.
的值大小关系.并说明理由.
通过你对以上问题的研究,请概括出在怎样的更一般的条件下,使得你研究的结果(即![]() 和
和![]() 的值大小关系)不变,并证明你的结论.
的值大小关系)不变,并证明你的结论.
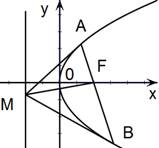
解析:(1)设过抛物线![]() 的焦点
的焦点![]() 的直线方程为
的直线方程为![]()
或![]() (斜率
(斜率![]() 不存在) ……………………1分
不存在) ……………………1分
则 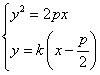 得
得 ![]()
![]() …………2分
…………2分
当![]() (斜率
(斜率![]() 不存在)时,则
不存在)时,则![]()
又![]()
![]() ……………………4分
……………………4分
![]() 所求抛物线方程为
所求抛物线方程为![]()
(2)[解] 设 
由已知直线![]() 、
、![]() 、
、![]() 的斜率分别记为:
的斜率分别记为:![]() 、
、![]() 、
、![]() ,得
,得
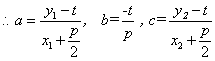 且
且 ![]() …………6分
…………6分
故![]()

![]()

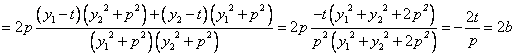
当![]() 时
时 ![]()
![]() 4 ………………10分
4 ………………10分
(文科) [解](3)![]() 和
和![]() 的值相等 …………12分
的值相等 …………12分
如果取![]() ,
,![]() 时, 则由(2)问得
时, 则由(2)问得 ![]()
![]()
![]()
![]()
![]() 即
即![]() , 又由(2)问得
, 又由(2)问得![]()
设![]()
1)若![]() 轴,则
轴,则![]() ……………………13分
……………………13分
2)若![]() >0 则
>0 则 ![]()
![]()
同理可得
![]()
而![]()
则 ![]() ,易知
,易知![]() 都是锐角
都是锐角
![]() …………………………16分
…………………………16分
3)若![]() <0,类似的也可证明
<0,类似的也可证明![]() .
.
综上所述![]() 即
即![]() 和
和![]() 的值相等 …………18分
的值相等 …………18分
(理科) [解](3)![]() 和
和![]() 的值相等 …………10分
的值相等 …………10分
如果取![]() ,
,![]() 时, 则由(2)问得
时, 则由(2)问得 ![]()
![]()
![]()
![]()
![]() 即
即![]() , 又由(2)问得
, 又由(2)问得![]()
设![]()
1)若![]() 轴,则
轴,则![]() ………………11分
………………11分
2)若![]() >0 则
>0 则 ![]()
![]()
同理可得
![]()
而![]()
即![]() ,易知
,易知![]() 都是锐角
都是锐角
![]() …………………………12分
…………………………12分
3)若![]() <0,类似的也可证明
<0,类似的也可证明![]() .
.
综上所述![]() 即
即![]() 和
和![]() 的值相等 …………13分
的值相等 …………13分
[解一](3)概括出的条件:![]()
![]() (即
(即![]() )或
)或![]() ,等
,等
…………………………14分
![]()
![]()
![]() 即
即![]() , 又由(2)问得
, 又由(2)问得![]()
设![]()
1)若![]() 轴,则
轴,则![]() ………………15分
………………15分
2)若![]() >0 则
>0 则 ![]()
同理可得![]()
而![]() ,则
,则![]() ;易知
;易知
![]() 都是锐角
都是锐角
![]() …………………………17分
…………………………17分
3)若![]() <0,类似的也可证明
<0,类似的也可证明![]() .
.
综上所述![]() 即
即![]() 和
和![]() 的值相等 ……18分
的值相等 ……18分
[解二] (略)(其它证法可参考上述评分标准给分)


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
(08年杨浦区测试)在等差数列![]() 中,公差
中,公差![]() ,且
,且![]() ,
,
(1)求![]() 的值.
的值.
(2)当![]() 时,在数列
时,在数列![]() 中是否存在一项
中是否存在一项![]() (
(![]() 正整数),使得
正整数),使得 ![]() ,
,![]() ,
,![]() 成等比数列,若存在,求
成等比数列,若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(3)若自然数![]() (
(![]() 为正整数)
为正整数)
满足![]() <
< ![]() <
<![]() <
< ![]() <
< ![]() <
<![]() , 使得
, 使得![]() 成等比数列,
成等比数列,
(文科考生做)当![]() 时, 用
时, 用![]() 表示
表示![]() .
.
(理科考生做)求![]() 的所有可能值.
的所有可能值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com