
【题目】已知![]() 三个顶点坐标分别为:
三个顶点坐标分别为:![]() ,直线
,直线![]() 经过点
经过点![]() .
.
(1)求![]() 外接圆
外接圆![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(3)若直线![]() 与
与![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)判断出三角形![]() 是等腰直角三角形,由此求得圆心和半径,进而求得
是等腰直角三角形,由此求得圆心和半径,进而求得![]() 的方程.
的方程.
(2)设出直线![]() 的方程,利用圆心到直线的距离等于半径,求得直线
的方程,利用圆心到直线的距离等于半径,求得直线![]() 的斜率,进而求得直线
的斜率,进而求得直线![]() 的方程.
的方程.
(3)当直线![]() 斜率不存在时,求得弦长
斜率不存在时,求得弦长![]() 符合题意.当直线
符合题意.当直线![]() 斜率存在时,设出直线
斜率存在时,设出直线![]() 的方程,利用弦长公式列方程,解方程求得直线
的方程,利用弦长公式列方程,解方程求得直线![]() 的斜率,由此求得直线
的斜率,由此求得直线![]() 的方程.
的方程.
(1)因为![]() ,所以
,所以![]() ,所以
,所以![]() ,且
,且![]() ,所以三角形
,所以三角形![]() 是等腰直角三角形,且
是等腰直角三角形,且![]() 为斜边,因而圆
为斜边,因而圆![]() 的圆心为
的圆心为![]() 的中点
的中点![]() ,半径为
,半径为![]() ,所以圆
,所以圆![]() 的方程为
的方程为![]() .
.
(2)当直线![]() 斜率不存在时,显然不合题意.当直线
斜率不存在时,显然不合题意.当直线![]() 的斜率存在时,设
的斜率存在时,设![]() ,即
,即![]() ,由题意知
,由题意知![]() ,解得
,解得![]() 或
或![]() .故直线
.故直线![]() 的方程为
的方程为![]() 或
或![]() .
.
(3)当直线![]() 斜率不存在时,将
斜率不存在时,将![]() 代入
代入![]() ,解得
,解得![]() ,即
,即![]() ,则
,则![]() ,符合题意.
,符合题意.
当直线![]() 斜率存在时,设
斜率存在时,设![]() ,即
,即![]() ,圆心
,圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,由
,由![]() 得
得![]() ,解得
,解得![]() ,故
,故![]() ,即
,即![]() .
.
所以直线![]() 的方程为
的方程为![]() 或
或![]() .
.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,曲线![]() :
: ![]() 经过伸缩变换
经过伸缩变换![]() 后得到曲线
后得到曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求出曲线![]() 、
、![]() 的参数方程;
的参数方程;
(Ⅱ)若![]() 、
、![]() 分别是曲线
分别是曲线![]() 、
、![]() 上的动点,求
上的动点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
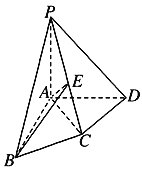
【题目】如图,在四棱锥![]() 中,PA⊥平面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.证明:
中,PA⊥平面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.证明:
(1)CD⊥AE;
(2)PD⊥平面ABE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin(ωx+φ)+1(![]() )的最小正周期为π,且
)的最小正周期为π,且![]() .
.
(1)求ω和φ的值;
(2)函数f(x)的图象纵坐标不变的情况下向右平移![]() 个单位,得到函数g(x)的图象,
个单位,得到函数g(x)的图象,
①求函数g(x)的单调增区间;
②求函数g(x)在![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若
,若![]() ,则称
,则称![]() 为
为![]() 的“不动点”,若
的“不动点”,若![]() ,则称
,则称![]() 为
为![]() 的“稳定点”,函数
的“稳定点”,函数![]() 的“不动点”和“稳定点”的集合分别记为
的“不动点”和“稳定点”的集合分别记为![]() 和
和![]() ,即
,即![]() ,那么,
,那么,
(1)求函数![]() 的“稳定点”;
的“稳定点”;
(2)若![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了引导居民合理用水,居民生活用水实行二级阶梯式水价计量方法,具体如下;第一阶梯,每户居民每月用水量不超过12吨,价格为4元/吨;第二阶梯,每户居民用水量超过12吨,超过部分的价格为8元/吨,为了了解全是居民月用水量的分布情况,通过抽样获得了100户居民的月用水量(单位:吨),将数据按照![]() (全市居民月用水量均不超过16吨)分成8组,制成了如图1所示的频率分布直方图.
(全市居民月用水量均不超过16吨)分成8组,制成了如图1所示的频率分布直方图.
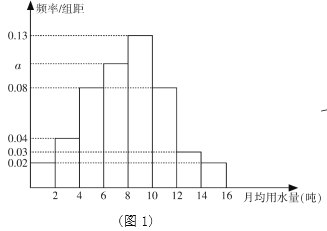
(Ⅰ)求频率分布直方图中字母![]() 的值,并求该组的频率;
的值,并求该组的频率;
(Ⅱ)通过频率分布直方图,估计该市居民每月的用水量的中位数![]() 的值(保留两位小数);
的值(保留两位小数);
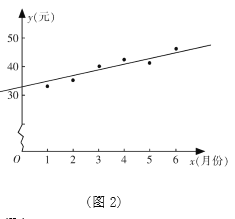
(Ⅲ)如图2是该市居民张某2016年1~6月份的月用水费![]() (元)与月份
(元)与月份![]() 的散点图,其拟合的线性回归方程是
的散点图,其拟合的线性回归方程是![]() 若张某2016年1~7月份水费总支出为312元,试估计张某7月份的用水吨数.
若张某2016年1~7月份水费总支出为312元,试估计张某7月份的用水吨数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com