
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且2asinA=(2b+c)sinB+(2c+b)sinC. (Ⅰ)求A的大小;
(Ⅱ)求sinB+sinC的最大值.
【答案】解:(Ⅰ)设 ![]() 则a=2RsinA,b=2RsinB,c=2RsinC
则a=2RsinA,b=2RsinB,c=2RsinC
∵2asinA=(2b+c)sinB+(2c+b)sinC
方程两边同乘以2R
∴2a2=(2b+c)b+(2c+b)c
整理得a2=b2+c2+bc
∵由余弦定理得a2=b2+c2﹣2bccosA
故cosA=﹣ ![]() ,A=120°
,A=120°
(Ⅱ)由(Ⅰ)得:sinB+sinC
=sinB+sin(60°﹣B)
= ![]() cosB+
cosB+ ![]() sinB
sinB
=sin(60°+B)
故当B=30°时,sinB+sinC取得最大值1
【解析】(Ⅰ)根据正弦定理,设 ![]() ,把sinA,sinB,sinC代入2asinA=(2b+c)sinB+(2c+b)sinC求出a2=b2+c2+bc 再与余弦定理联立方程,可求出cosA的值,进而求出A的值.(Ⅱ)根据(Ⅰ)中A的值,可知c=60°﹣B,化简得sin(60°+B)根据三角函数的性质,得出最大值.
,把sinA,sinB,sinC代入2asinA=(2b+c)sinB+(2c+b)sinC求出a2=b2+c2+bc 再与余弦定理联立方程,可求出cosA的值,进而求出A的值.(Ⅱ)根据(Ⅰ)中A的值,可知c=60°﹣B,化简得sin(60°+B)根据三角函数的性质,得出最大值.


科目:高中数学 来源: 题型:
【题目】某市对创“市级示范性学校”的甲、乙两所学校进行复查验收,对办学的社会满意度一项评价随机访问了20为市民,这20位市民对这两所学校的评分(评分越高表明市民的评价越好)的数据如下:
甲校:58,66,71,58,67,72,82,92,83,86,67,59,86,72,78,59,68,69,73,81;
乙校:90,80,73,65,67,69,81,85,82,88,89,86,86,78,98,95,96,91,76,69,.
检查组将成绩分成了四个等级:成绩在区间![]() 的为
的为![]() 等,在区间
等,在区间![]() 的为
的为![]() 等,在区间
等,在区间![]() 的为
的为![]() 等,在区间
等,在区间![]() 为
为![]() 等.
等.
(1)请用茎叶图表示上面的数据,并通过观察茎叶图,对两所学校办学的社会满意度进行比较,写出两个统计结论;
(2)根据所给数据,以事件发生的频率作为相应事件发生的概率,求乙校得分的等级高于甲校得分的等级的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 的左、右焦点,
的左、右焦点, ![]() 为坐标原点,点
为坐标原点,点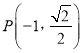 在椭圆上,线段
在椭圆上,线段![]() 与
与![]() 轴的交点
轴的交点![]() 满足
满足![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)圆![]() 是以
是以![]() 为直径的圆,一直线
为直径的圆,一直线![]() 与圆
与圆![]() 相切,并与椭圆交于不同的两点
相切,并与椭圆交于不同的两点![]() 、
、![]() ,当
,当![]() ,且满足
,且满足![]() 时,求
时,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥![]() ,
,![]() ,侧面
,侧面![]() 是边长为4的等边三角形,底面
是边长为4的等边三角形,底面![]() 为菱形,侧面
为菱形,侧面![]() 与底面
与底面![]() 所成的二面角为
所成的二面角为![]() .
.
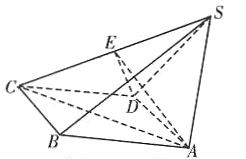
(1)求点![]() 到平面
到平面![]() 的距离;
的距离;
(2)若![]() 为
为![]() 的中点,求二面角
的中点,求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ),
),![]() 为
为![]() 上一点,以
上一点,以![]() 为边作等边三角形
为边作等边三角形![]() ,且
,且![]() 、
、![]() 、
、![]() 三点按逆时针方向排列.
三点按逆时针方向排列.
(Ⅰ)当点![]() 在
在![]() 上运动时,求点
上运动时,求点![]() 运动轨迹的直角坐标方程;
运动轨迹的直角坐标方程;
(Ⅱ)若曲线![]() :
: ![]() ,经过伸缩变换
,经过伸缩变换![]() 得到曲线
得到曲线![]() ,试判断点
,试判断点![]() 的轨迹与曲线
的轨迹与曲线![]() 是否有交点,如果有,请求出交点的直角坐标,没有则说明理由.
是否有交点,如果有,请求出交点的直角坐标,没有则说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com