
【题目】某同学用“五点法”画函数![]() 在某一周期内的图像时,列表并填入的部分数据如下表:
在某一周期内的图像时,列表并填入的部分数据如下表:
|
|
|
|
|
|
| 0 |
|
|
|
|
| 0 | 1 | 0 |
| 0 |
| 0 |
| 0 |
| 0 |
(1)请写出上表的![]() 及函数
及函数![]() 的解析式;
的解析式;
(2)将函数![]() 的图像向右平移
的图像向右平移![]() 个单位,再将所得图像上各点的横坐标缩小为原来的
个单位,再将所得图像上各点的横坐标缩小为原来的![]() ,纵坐标不变,得到函数
,纵坐标不变,得到函数![]() 的图像,求
的图像,求![]() 的解析式及
的解析式及 的单调递增区间;
的单调递增区间;
(3)在(2)的条件下,若![]() 在
在![]() 上恰有奇数个零点,求实数
上恰有奇数个零点,求实数![]() 与零点个数
与零点个数![]() 的值.
的值.
【答案】(1)![]() ;
;
(2)![]() ;
;
(3)![]() .
.
【解析】
(1)根据表中数据可得关于![]() 的方程组,解出
的方程组,解出![]() 的值后可得
的值后可得![]() 的值,再由表中数据可得
的值,再由表中数据可得![]() ,从而可得函数的解析式.
,从而可得函数的解析式.
(2)先求出![]() 的解析式,再求出
的解析式,再求出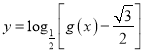 的定义域,结合三角函数的单调性可得复合函数的单调增区间.
的定义域,结合三角函数的单调性可得复合函数的单调增区间.
(3)令![]() ,设方程
,设方程![]() 的根为
的根为![]() ,分①
,分①![]() ;②
;②![]() ;③
;③![]() 三种情况讨论
三种情况讨论![]() 在
在![]() 及
及![]() 上零点个数,再根据周期性得到
上零点个数,再根据周期性得到![]() 的零点个数,结合题设条件可得
的零点个数,结合题设条件可得![]() 的值及相应的零点个数.
的值及相应的零点个数.
(1)根据表中的数据可得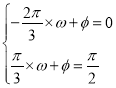 ,解得
,解得 ,
,
故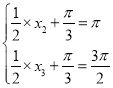 ,所以
,所以 ,又
,又![]() ,故
,故![]() .
.
所以![]() .
.
(2)将函数![]() 的图像向右平移
的图像向右平移![]() 个单位,所得图像的解析式为:
个单位,所得图像的解析式为:
![]() ,
,
再将所得图像上各点的横坐标缩小为原来的![]() ,纵坐标不变,得到函数
,纵坐标不变,得到函数![]() 的图像,
的图像,
故![]() .
.
此时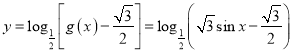 ,
,
令![]() ,则
,则![]() ,故
,故![]() .
.
当![]() 时,
时,![]() 为增函数,
为增函数,
故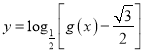 为减函数;
为减函数;
当![]() 时,
时,![]() 为减函数;
为减函数;
故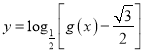 为增函数.
为增函数.
所以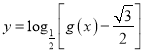 的增区间为
的增区间为![]() .
.
(3)![]() ,
,![]() 的周期为
的周期为![]() ,
,
当![]() 时,令
时,令![]() ,考虑方程
,考虑方程![]() 的根情况,
的根情况,
因![]() ,故
,故![]() 在
在![]() 必有两个不同的实数根
必有两个不同的实数根![]() ,
,
因为![]() 在
在![]() 有奇数个零点,故
有奇数个零点,故![]() 或
或![]() .
.
若![]() ,则方程
,则方程![]() 、
、![]() 在
在![]() 共有4个不同的实数根,
共有4个不同的实数根,
在![]() 有0个实数根或2个实数根,
有0个实数根或2个实数根,
故![]() 在
在![]() 有
有![]() 个根或
个根或![]() 个根,
个根,
与![]() 有奇数个零点矛盾,舍去.
有奇数个零点矛盾,舍去.
若![]() ,则
,则![]() 在
在![]() 共有2个不同的实数根,在
共有2个不同的实数根,在![]() 有0个实数根或2个实数根,
有0个实数根或2个实数根,
故![]() 在
在![]() 有
有
![]() 个根或
个根或![]() ,
,
与![]() 有奇数个零点矛盾,舍去.
有奇数个零点矛盾,舍去.
同理![]() 也不成立,所以
也不成立,所以![]() 或
或![]() ,
,
若![]() ,则
,则![]() ,
,![]() ,
,
方程![]() 、
、![]() 在
在![]() 共有3个不同的实数根,而在
共有3个不同的实数根,而在![]() 上,
上,![]() 有两个不同的根,
有两个不同的根,![]() 无解,
无解,
所以![]() 在
在![]() 有
有![]() 个根,符合要求;
个根,符合要求;
若![]() ,则
,则![]() ,
,![]() ,
,
方程![]() 、
、![]() 在
在![]() 共有3个不同的实数根,而在
共有3个不同的实数根,而在![]() 上,
上,![]() 无解,
无解,![]() 有一个根,
有一个根,
所以故![]() 在
在![]() 有
有![]() 个根,与题设矛盾,舍去.
个根,与题设矛盾,舍去.
综上,![]() ,
,![]() 在
在![]() 共有
共有![]() 个不同的零点.
个不同的零点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某知名品牌汽车深受消费者喜爱,但价格昂贵.某汽车经销商推出A、B、C三种分期付款方式销售该品牌汽车,并对近期100位采用上述分期付款的客户进行统计分析,得到如下的柱状图.已知从A、B、C三种分期付款销售中,该经销商每销售此品牌汽车1俩所获得的利润分别是1万元,2万元,3万元.现甲乙两人从该汽车经销商处,采用上述分期付款方式各购买此品牌汽车一辆.以这100位客户所采用的分期付款方式的频率代替1位客户采用相应分期付款方式的概率.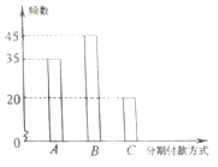
(1)求甲乙两人采用不同分期付款方式的概率;
(2)记X(单位:万元)为该汽车经销商从甲乙两人购车中所获得的利润,求X的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015![]() 全国统考II)设函数f(x)=ln(1+|x|)-
全国统考II)设函数f(x)=ln(1+|x|)-![]() ,则使得f(x)
,则使得f(x)![]() f(2x-1)成立的x的取值范围是()
f(2x-1)成立的x的取值范围是()
A.(![]() ,1)
,1)
B.(-![]() ,
,![]() )
)![]() (1,+
(1,+![]() )
)
C.(-![]() ,
,![]() )
)
D.(-![]() ,-
,-![]() )
)![]() (
(![]() ,+
,+![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 在直角坐标系xOy中,曲线C1:
在直角坐标系xOy中,曲线C1:![]() (t为参数,且t≠0),其中0
(t为参数,且t≠0),其中0![]()
![]()
![]() , 在以O为极点x轴正半轴为极轴的极坐标系中,曲线C2::
, 在以O为极点x轴正半轴为极轴的极坐标系中,曲线C2::![]() =2sin
=2sin![]() , C3:
, C3:![]() =2
=2![]() cos
cos![]()
(1)求C2与C3交点的直角坐标
(2)若C1与C2相交于点A,C1与C3相交于点B,求|AB|最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅行社组织一批游客外出旅游,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满,已知45座客车租金为每辆220元,60座客车租金为每辆300元,问:
(1)这批游客的人数是多少?原计划租用多少辆45座客车?
(2)若租用同一种车,要使每位游客都有座位,应该怎样租用才合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·新课标I卷)如图,四边形ABCD为菱形,∠ABC=120°,E , F是平面ABCD同一侧的两点,BE⊥平面ABCD , DF⊥平面ABCD , BE=2DF , AE⊥EC.
(1)证明:平面AEC⊥平面AFC
(2)求直线AE与直线CF所成角的余弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·四川)已知函数f(x)=2x , g(x)=x2+ax(其中a![]() R).对于不相等的实数x1, x2 , 设m=
R).对于不相等的实数x1, x2 , 设m=![]() ,n=
,n=![]() .
.
现有如下命题:
(1)对于任意不相等的实数x1, x2 , 都有m>0;
(2)对于任意的a及任意不相等的实数x1, x2 , ,都有n>0;
(3)对于任意的a , 存在不相等的实数x1, x2 , 使得m=n;
(4)对于任意的a , 存在不相等的实数x1, x2 , 使得m=-n.
其中的真命题有 (写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖南)某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖,抽奖方法是:从装有2个红球A1, A2和1个白球B的甲箱与装有2个红球a1,a2和2个白球b1,b2的乙箱中,各随机摸出1个球,若摸出的2个球都是红球则中奖,否则不中奖。
(1)用球的标号列出所有可能的摸出结果;
(2)有人认为:两个箱子中的红球比白球多,所以中奖的概率大于不中奖的概率,你认为正确吗?请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com