
分析 (Ⅰ)解$\left\{\begin{array}{l}{3+2x>0}\\{3-2x>0}\end{array}\right.$可解函数F(x)的定义域;
(Ⅱ)由(Ⅰ)可知定义域关于原点对称,由奇函数的定义可证;
(Ⅲ)问题转化为loga(3+2x)>loga(3-2x),针对a结合对数函数的单调性分类讨论可得.
解答 解:(Ⅰ)F(x)=f(x)-g(x)=loga(3+2x)-loga(3-2x),
由$\left\{\begin{array}{l}{3+2x>0}\\{3-2x>0}\end{array}\right.$,可解得:$-\frac{3}{2}<x<\frac{3}{2}$,
∴函数F(x)的定义域为$\left\{{x|-\frac{3}{2}<x<\frac{3}{2}}\right\}$;
(Ⅱ)由(Ⅰ)可知函数F(x)的定义域为$\left\{{x|-\frac{3}{2}<x<\frac{3}{2}}\right\}$关于原点对称,
且F(-x)=f(-x)-g(-x)=loga(3-2x)-loga(3+2x)=-F(x)
∴函数F(x)为奇函数;
(Ⅲ)∵f(x)-g(x)>0,∴loga(3+2x)-loga(3-2x)>0,
∴loga(3+2x)>loga(3-2x),分类讨论可得:
①当0<a<1时,由3+2x<3-2x结合定义域可解得$-\frac{3}{2}<x<0$;
②当a>1时,由3+2x>3-2x结合定义域解得$0<x<\frac{3}{2}$.
综上:当0<a<1时,不等式的解集为$\left\{{x|-\frac{3}{2}<x<0}\right\}$;
当a>1时,不等式的解集为$\left\{{x|0<x<\frac{3}{2}}\right\}$.
点评 本题考查对数函数的图象和性质,涉及分类讨论的思想,属基础题.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
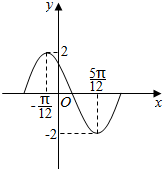 函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π)在一个周期内的图象如图,此函数的解析式为y=2sin(2x+$\frac{2π}{3}$).
函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π)在一个周期内的图象如图,此函数的解析式为y=2sin(2x+$\frac{2π}{3}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,一根长为2米的竹竿AB斜靠在在直角墙壁上,假设竹竿在同一平面内移动,当竹竿的下段点A从距离墙角O点1米的地方移动到$\sqrt{3}$米的地方,则AB的中点D经过的路程为$\frac{π}{6}$米.
如图,一根长为2米的竹竿AB斜靠在在直角墙壁上,假设竹竿在同一平面内移动,当竹竿的下段点A从距离墙角O点1米的地方移动到$\sqrt{3}$米的地方,则AB的中点D经过的路程为$\frac{π}{6}$米.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{10}$ | B. | $\frac{7}{10}$ | C. | $\frac{\sqrt{5}}{20}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -9 | B. | -1 | C. | 1 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com