
【题目】高一(1)班参加校生物竞赛学生的成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:
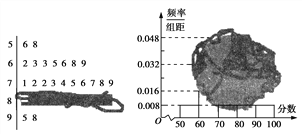
(1)求高一(1)班参加校生物竞赛的人数及分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(2)若要从分数在[80,100]之间的学生中任选2人进行某项研究,求至少有1人分数在[90,100]之间的概率.
【答案】(1)0. 016;(2)![]()
【解析】试题分析:(1)根据频率等于频数除以总数,可得到参加校生物竞赛的人数,再根据分数在[80,90)之间的频率求频数,根据矩形高等于对应频率除以组距得高(2)先根据枚举法列出所有基本事件,再计数至少有1人分数在[90,100]之间基本试卷数,最后根据古典概型概率公式求概率
试题解析: (1)因为分数在[50,60)之间的频数为2,频率为0. 008×10=0. 08,所以高一(1)班参加校生物竞赛的人数为![]() =25.
=25.
分数在[80,90)之间的频数为25-2-7-10-2=4,频率为![]() =0. 16,
=0. 16,
所以频率分布直方图中[80,90)间的矩形的高为![]() =0. 016.
=0. 016.
(2)设“至少有1人分数在[90,100]之间”为事件A,将[80,90)之间的4人编号为1、2、3、4,[90,100]之间的2人编号为5、6.
在[80,100]之间任取2人的基本事件有:(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6),共15个.其中,至少有1人分数在[90,100]之间的基本事件有9个,
根据古典概型概率的计算公式,得P(A)=![]() =
=![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在三棱台ABC﹣DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.
(1)求证:BF⊥平面ACFD;
(2)求直线BD与平面ACFD所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下是新兵训练时,某炮兵连8周中炮弹对同一目标的命中情况的柱状图: 
(1)计算该炮兵连这8周中总的命中频率p0 , 并确定第几周的命中频率最高;
(2)以(1)中的p0作为该炮兵连炮兵甲对同一目标的命中率,若每次发射相互独立,且炮兵甲发射3次,记命中的次数为X,求X的数学期望;
(3)以(1)中的p0作为该炮兵连炮兵对同一目标的命中率,试问至少要用多少枚这样的炮弹同时对该目标发射一次,才能使目标被击中的概率超过0.99?(取lg0.4=﹣0.398)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在高为2的梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,过
,过![]() 、
、![]() 分别作
分别作![]() ,
, ![]() ,垂足分别为
,垂足分别为![]() 、
、![]() 。已知
。已知![]() ,将梯形
,将梯形![]() 沿
沿![]() 、
、![]() 同侧折起,得空间几何体
同侧折起,得空间几何体![]() ,如图2。
,如图2。

(1)若![]() ,证明:
,证明: ![]() ;
;
(2)若![]() ,证明:
,证明: ![]() ;
;
(3)在(1),(2)的条件下,求三棱锥![]() 的体积。
的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,焦点
的中心在原点,焦点![]() 、
、![]() 在
在![]() 轴上,离心率为
轴上,离心率为![]() ,在椭圆
,在椭圆![]() 上有一动点
上有一动点![]() 与
与![]() 、
、![]() 的距离之和为4,
的距离之和为4,
(Ⅰ) 求椭圆E的方程;
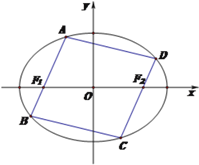
(Ⅱ) 过![]() 、
、![]() 作一个平行四边形,使顶点
作一个平行四边形,使顶点![]() 、
、![]() 、
、![]() 、
、![]() 都在椭圆
都在椭圆![]() 上,如图所示.判断四边形
上,如图所示.判断四边形![]() 能否为菱形,并说明理由.
能否为菱形,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车给市民出行带来了诸多便利,某公司购买了一批单车投放到某地给市民使用,
据市场分析,每辆单车的营运累计利润y(单位:元)与营运天数x![]() 满足函数关系
满足函数关系
式![]() .
.
(1)要使营运累计利润高于800元,求营运天数的取值范围;
(2)每辆单车营运多少天时,才能使每天的平均营运利润![]() 的值最大?
的值最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
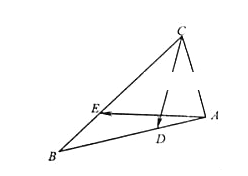
【题目】如图,在△ABC中,已知CA=1,CB=2,∠ACB=60°.
(1)求|![]() |;
|;
(2)已知点D是AB上一点,满足![]() =λ
=λ![]() ,点E是边CB上一点,满足
,点E是边CB上一点,满足![]() =λ
=λ![]() .
.
①当λ=![]() 时,求
时,求![]()
![]() ;
;
②是否存在非零实数λ,使得![]() ⊥
⊥![]() ?若存在,求出的λ值;若不存在,请说明理由.
?若存在,求出的λ值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx﹣ ![]() x2(a∈R).
x2(a∈R).
(1)若x>0,恒有f(x)≤x成立,求实数a的取值范围;
(2)若a=0,求f(x)在区间[t,t+2](t>0)上的最小值;
(3)若函数g(x)=f(x)﹣x有两个极值点x1 , x2 , 求证: ![]() +
+ ![]() >2ae.
>2ae.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com