Question

甲、乙两人参加普法知识竞赛，共设有10个不同的题目，其中选择题6个，判断题4个，
（Ⅰ）若甲、乙二人依次各抽一题，计算：
①甲抽到判断题，乙抽到选择题的概率是多少？
②甲、乙二人中至少有一人抽到选择题的概率是多少？
（Ⅱ）若甲从中随机抽取5个题目，其中判断题的个数为ξ，求ξ的分布列和期望．

Answer 1

分析：（Ⅰ）由题意知本题可以看做等可能事件的概率，试验发生包含的事件数A₁₀²，①满足条件的事件是甲抽到选择题，乙抽到判断题，共有C₆¹C₄¹种结果，②满足条件的事件是甲、乙二人中至少有一人抽到选择题，共有A₆²+C₆¹C₄¹+C₄¹C₆¹种结果，根据概率公式得到结果．
（Ⅱ）甲从中随机抽取5个题目，其中判断题的个数为ξ，ξ可取0、1、2、3、4，结合变量对应的事件写出变量对应的概率，写出分布列和期望．

解答：解：（Ⅰ）由题意知本题可以看做等可能事件的概率，
试验发生包含的事件数A₁₀²，
①满足条件的事件是甲抽到选择题，乙抽到判断题，共有C₆¹C₄¹种结果，
∴P（A）=

C 1 6 • C 1 4

A 2 10

=

4

15

②满足条件的事件是甲、乙二人中至少有一人抽到选择题，共有A₆²+C₆¹C₄¹+C₄¹C₆¹种结果
∴概率P（B）=

A 2 6 + C 1 6 • C 1 4 +  C 1 4 • C 1 6

A 2 10

=

13

15

（Ⅱ）甲从中随机抽取5个题目，其中判断题的个数为ξ，ξ可取0、1、2、3、4
P（ξ）=

C 5 6 • C 0 4

A 5 10

=

1

42

；P（ξ=1）=

C 4 6 • C 1 4

A 5 10

=

5

21

；
P（ξ=2）=

C 3 6 • C 2 4

A 5 10

=

10

21

；P（ξ=3）=

C 2 6 • C 3 4

A 5 10

=

5

21

；
P（ξ=4）=

C 1 6 • C 4 4

A 5 10

=

1

42

．
∴ξ的分布列为

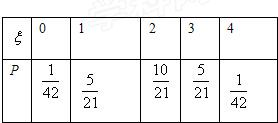
∴E_ξ=0×

1

42

+1×

5

21

+2×

10

21

+3×

5

21

+4×

1

42

=

84

42

=2．

点评：本题考查等可能事件的概率，考查离散型随机变量的分布列和期望，是一个综合题，本题的知识点和难易程度，可以作为一个高考题的解答题目出现．