
分析 (1)法一:由奇函数的性质:f(0)=0列出方程,化简后求出m的值;
法二:由奇函数的性质:f(x)+f(-x)=0列出方程组,化简后求出m的值;
(2)利用指数函数的单调性,以及函数单调性的定义:取值、作差、变形、定号、下结论进行证明.
解答 解:(1)法一:由函数f(x)为奇函数,得f(0)=0即m+1=0,
所以m=-1…(5分)
法二:因为函数f(x)为奇函数,所以f(-x)=-f(x),
即f(-x)+f(x)=0…(2分)
∴$f({-x})+f(x)=({m+\frac{2}{{{2^{-x}}+1}}})+({m+\frac{2}{{{2^x}+1}}})=2m+({\frac{2}{{\frac{1}{2^x}+1}}+\frac{2}{{{2^x}+1}}})$
=$2m+({\frac{{2•{2^x}}}{{1+{2^x}}}+\frac{2}{{{2^x}+1}}})=2m+\frac{{2•({{2^x}+1})}}{{1+{2^x}}}=2m+2=0$,
所以m=-1…(5分)
(2)证明:任取x1,x2∈R,且x1<x2…(6分)
则$f({x}_{1})-f({x}_{2})=(m+\frac{2}{{2}^{{x}_{1}}+1})-(m+\frac{2}{{2}^{{x}_{2}}+1})$
=$\frac{2}{{2}^{{x}_{2}}+1}-\frac{2}{{2}^{{x}_{1}}+1}=\frac{2•({2}^{{x}_{2}}-{2}^{{x}_{1}})}{({2}^{{x}_{1}}+1)•({2}^{{x}_{2}}+1)}$ …(8分)
∵x1<x2,∴${2^{x_1}}-{2^{x_2}}<0$,${2^{x_2}}+1>0$,∴${2^{x_1}}+1>0$,
f(x1)-f(x2)>0,即f(x1)>f(x2)…(10分)
所以,对任意的实数m,函数f(x)在(-∞,+∞)上是减函数…(12分)
点评 本题考查了奇函数的性质,利用单调性的定义证明函数的单调性,考查方程思想,函数思想,化简、变形能力.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:填空题
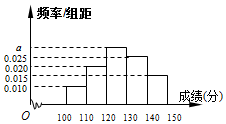 某学校对高二年级期中考试数学成绩进行分析,随机抽取了分数在[100,150]的1000名学生的成绩,并根据这1000名学生的成绩画出频率分布直方图(如图所示),则成绩在[120,130)内的学生共有300人.
某学校对高二年级期中考试数学成绩进行分析,随机抽取了分数在[100,150]的1000名学生的成绩,并根据这1000名学生的成绩画出频率分布直方图(如图所示),则成绩在[120,130)内的学生共有300人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x2-2x+1 | B. | f(x)=x2-1 | C. | f(x)=2x | D. | f(x)=2x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com