
【题目】已知椭圆的中心在原点,焦点在![]() 轴上,一个顶点
轴上,一个顶点![]() ,且右焦点到直线
,且右焦点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆的方程.
(2)若点![]() 为椭圆的下顶点,是否存在斜率为
为椭圆的下顶点,是否存在斜率为![]() ,且过定点
,且过定点![]() 的直线
的直线![]() ,使
,使![]() 与椭圆交于不同两点
与椭圆交于不同两点![]() ,
,![]() 且满足
且满足![]() ? 若存在,求直线
? 若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:
【题目】如图是2018年第一季度五省GDP情况图,则下列描述中不正确的是( )

A. 与去年同期相比2018年第一季度五个省的GDP总量均实现了增长
B. 2018年第一季度GDP增速由高到低排位第5的是浙江省
C. 2018年第一季度GDP总量和增速由高到低排位均居同一位的省只有1个
D. 去年同期河南省的GDP总量不超过4000亿元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() (
(![]() 为参数).以
为参数).以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程及直线
的方程及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了了解2018年当地居民网购消费情况,随机抽取了100人,对其2018年全年网购消费金额(单位:千元)进行了统计,所统计的金额均在区间![]() 内,并按
内,并按![]() ,
,![]() ,…,
,…,![]() 6组,制成如图所示的频率分布直方图.
6组,制成如图所示的频率分布直方图.
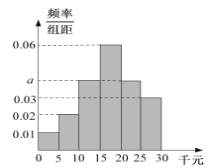
(1)求图中![]() 的值;
的值;
(2)若将全年网购消费金额在20千元及以上者称为网购迷.结合图表数据,补全![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为样本数据中的网购迷与性别有关系?说明理由;
的把握认为样本数据中的网购迷与性别有关系?说明理由;
男 | 女 | 合计 | |
网购迷 | 20 | ||
非网购迷 | 45 | ||
合计 |
下面的临界值表仅供参考:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
附:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数, ![]() 为自然对数的底数),曲线
为自然对数的底数),曲线![]() 在与
在与![]() 轴的交点
轴的交点![]() 处的切线斜率为-1.
处的切线斜率为-1.
(1)求![]() 的值及函数
的值及函数![]() 的单调区间;
的单调区间;
(2)证明:当![]() 时,
时, ![]() ;
;
(3)证明:当![]() 时,
时, 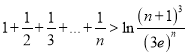 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地4个蔬菜大棚顶部,阳光照在一棵棵茁壮生长的蔬菜上,这些采用水培、无土栽培方式种植的各类蔬菜,成为该地区居民争相购买的对象,过去50周的资料显示,该地周光照量![]() (小时)都在30以上,其中不足50的周数大约5周,不低于50且不超过70的周数大约有35周,超过70的大约有10周,根据统计某种改良黄瓜每个蔬菜大棚增加量
(小时)都在30以上,其中不足50的周数大约5周,不低于50且不超过70的周数大约有35周,超过70的大约有10周,根据统计某种改良黄瓜每个蔬菜大棚增加量![]() (百斤)与每个蔬菜大棚使用农夫1号液体肥料
(百斤)与每个蔬菜大棚使用农夫1号液体肥料![]() (千克)之间对应数据为如图所示的折线图.
(千克)之间对应数据为如图所示的折线图.
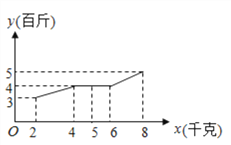
(1)依据数据的折线图,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;并根据所求线性回归方程,估计如果每个蔬菜大棚使用农夫1号肥料10千克,则这种改良黄瓜每个蔬菜大鹏增加量
;并根据所求线性回归方程,估计如果每个蔬菜大棚使用农夫1号肥料10千克,则这种改良黄瓜每个蔬菜大鹏增加量![]() 是多少斤?
是多少斤?
(2)因蔬菜大棚对光照要求较大,某光照控制仪商家为应对恶劣天气对光照的影响,为该基地提供了部分光照控制仪,该商家希望安装的光照控制仪尽可能运行,但每周光照控制仪最多可运行台数受周光照量![]() 限制,并有如下关系:
限制,并有如下关系:
周光照量 | 30<X<50 |
|
|
光照控制仪最多可运行台数 | 3 | 2 | 1 |
若某台光照控制仪运行,则该台光照仪周利润为4000元;若某台光照仪未运行,则该台光照仪周亏损500元,欲使商家周总利润的均值达到最大,应安装光照控制仪多少台?
附:回归方程系数公式: 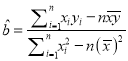 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1}.
(1)若A∪B=A,求实数m的取值范围;
(2)当x∈Z时,求A的非空真子集的个数;
(3)当x∈R时,若A∩B=,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com