
【题目】某市2011年至2017年新开楼盘的平均销售价格(单位:千元/平方米)的统计数据如下表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格 | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
附:参考公式: ,
,![]() ,其中
,其中![]() 为样本平均值。
为样本平均值。
参考数据:![]() ,
,![]() .
.
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析2011年至2017年该市新开楼盘平均销售价格的变化情况,并预测该市2019年新开楼盘的平均销售价格。
 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程](10分)
在极坐标系中,圆C的极坐标方程为![]() ,若以极点O为原点,极轴为x轴的正半轴建立平面直角坐标系.
,若以极点O为原点,极轴为x轴的正半轴建立平面直角坐标系.
(1)求圆C的一个参数方程;
(2)在平面直角坐标系中,![]() 是圆C上的动点,试求
是圆C上的动点,试求![]() 的最大值,并求出此时点P的直角坐标.
的最大值,并求出此时点P的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社区组织“学习强国”的知识竞赛,从参加竞赛的市民中抽出40人,将其成绩分成以下6组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,第6组
,第6组![]() ,得到如图所示的频率分布直方图.现采用分层抽样的方法,从第2,3,4组中按分层抽样抽取8人,则第2,3,4组抽取的人数依次为( )
,得到如图所示的频率分布直方图.现采用分层抽样的方法,从第2,3,4组中按分层抽样抽取8人,则第2,3,4组抽取的人数依次为( )
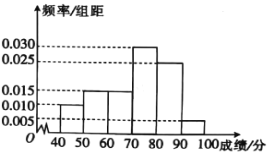
A.1,3,4B.2,3,3C.2,2,4D.1,1,6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司计划在甲、乙两座城市共投资240万元,根据行业规定,每个城市至少要投资80万元,由前期市场调研可知:甲城市收益![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,乙城市收益
,乙城市收益![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足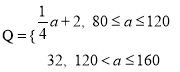 ,设甲城市的投入为
,设甲城市的投入为![]() (单位:万元),两个城市的总收益为
(单位:万元),两个城市的总收益为![]() (单位:万元).
(单位:万元).
(1)当投资甲城市128万元时,求此时公司总收益;
⑵试问如何安排甲、乙两个城市的投资,才能使公司总收益最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了鼓励大家节约用水,自2013年以后,上海市实行了阶梯水价制度,其中每户的综合用水单价与户年用水量的关系如下表所示.
分档 | 户年用水量 | 综合用水单价/(元· |
第一阶梯 | 0 | 3.45 |
第二阶梯 | 220 | 4.83 |
第三阶梯 | 300以上 | 5.83 |
记户年用水量为![]() 时应缴纳的水费为
时应缴纳的水费为![]() 元.
元.
(1)写出![]() 的解析式;
的解析式;
(2)假设居住在上海的张明一家2015年共用水![]() ,则张明一家2015年应缴纳水费多少元?
,则张明一家2015年应缴纳水费多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,
,![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项的和.
项的和.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列,![]() ,18,
,18,![]() 成等比数列,求正整数
成等比数列,求正整数![]() 的值;
的值;
(3)是否存在![]() ,使得
,使得![]() 为数列
为数列![]() 中的项?若存在,求出所有满足条件的
中的项?若存在,求出所有满足条件的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD中,已知AB=a,BC=b(a>b),在AB,AD,CB,CD上,分别截取AE=AH=CF=CG=x(x>0),设四边形EFGH的面积为y.
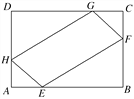
(1)写出四边形EFGH的面积y与x之间的函数关系;
(2)求当x为何值时y取得最大值,最大值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() :
: (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的直角坐标为
的直角坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com