
【题目】已知函数f(x)=|2x﹣a|+|x﹣a+1|.
(1)当a=4时,求解不等式f(x)≥8;
(2)已知关于x的不等式f(x)![]() 在R上恒成立,求参数a的取值范围.
在R上恒成立,求参数a的取值范围.
【答案】(1)[5,+∞)∪(∞,![]() ];(2)[﹣2,1].
];(2)[﹣2,1].
【解析】
(1)根据a=4时,有f(x)=|2x﹣4|+|x﹣3|,然后利用绝对值的几何意义,去绝对值求解.
(2)根据绝对值的零点有a﹣1和![]() ,分a﹣1
,分a﹣1![]() ,a﹣1
,a﹣1![]() 和a﹣1
和a﹣1![]() 时三种情况分类讨论求解.
时三种情况分类讨论求解.
(1)当a=4时,f(x)=|2x﹣4|+|x﹣3|,
(i)当x≥3时,原不等式可化为3x﹣7≥8,解可得x≥5,
此时不等式的解集[5,+∞);
(ii)当2<x<3时,原不等式可化为2x﹣4+3﹣x≥8,解可得x≥9
此时不等式的解集;
(iii)当x≤2时,原不等式可化为﹣3x+7≥8,解可得x![]() ,
,
此时不等式的解集(∞,![]() ],
],
综上可得,不等式的解集[5,+∞)∪(∞,![]() ],
],
(2)(i)当a﹣1![]() 即a=2时,f(x)=3|x﹣1|
即a=2时,f(x)=3|x﹣1|![]() 2显然不恒成立,
2显然不恒成立,
(ii)当a﹣1![]() 即a>2时,
即a>2时,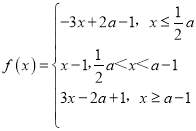 ,
,
结合函数的单调性可知,当x![]() 时,函数取得最小值f(
时,函数取得最小值f(![]() )
)![]() ,
,
若f(x)![]() 在R上恒成立,则
在R上恒成立,则![]() ,此时a不存在,
,此时a不存在,
(iii)当a﹣1![]() 即a<2时,f(x)
即a<2时,f(x)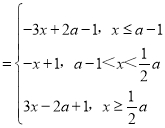
若f(x)![]() 在R上恒成立,则1
在R上恒成立,则1![]() ,
,
解得﹣2≤a≤1,
此时a的范围[﹣2,1],
综上可得,a的范围围[﹣2,1].


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】某中学为了解中学生的课外阅读时间,决定在该中学的1200名男生和800名女生中按分层抽样的方法抽取20名学生,对他们的课外阅读时间进行问卷调查.现在按课外阅读时间的情况将学生分成三类:![]() 类(不参加课外阅读),
类(不参加课外阅读),![]() 类(参加课外阅读,但平均每周参加课外阅读的时间不超过3小时),
类(参加课外阅读,但平均每周参加课外阅读的时间不超过3小时),![]() 类(参加课外阅读,且平均每周参加课外阅读的时间超过3小时).调查结果如下表:
类(参加课外阅读,且平均每周参加课外阅读的时间超过3小时).调查结果如下表:
|
|
| |
男生 |
| 5 | 3 |
女生 |
| 3 | 3 |
(1)求出表中![]() ,
,![]() 的值;
的值;
(2)根据表中的统计数据,完成下面的列联表,并判断是否有90%的把握认为“参加课外阅读与否”与性别有关;
男生 | 女生 | 总计 | ||
不参加课外阅读 | ||||
参加课外阅读 | ||||
总计 |
P(K≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】半正多面体(semiregular solid) 亦称“阿基米德多面体”,是由边数不全相同的正多边形为面的多面体,体现了数学的对称美.二十四等边体就是一种半正多面体,是由正方体切截而成的,它由八个正三角形和六个正方形为面的半正多面体.如图所示,图中网格是边长为1的正方形,粗线部分是某二十四等边体的三视图,则该几何体的体积为( )
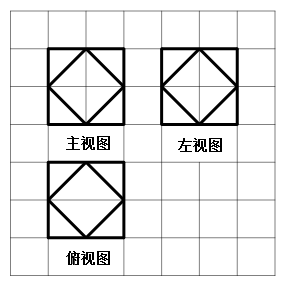
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为a的正方体ABCD﹣A1B1C1D1中,P,Q,L分别为棱A1D1,C1D1,BC的中点.
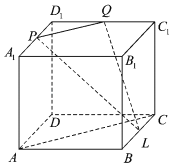
(1)求证:AC⊥QL;
(2)求四面体DPQL的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年12月以来,湖北武汉市发现多起病毒性肺炎病例,并迅速在全国范围内开始传播,专家组认为,本次病毒性肺炎病例的病原体初步判定为新型冠状病毒,该病毒存在人与人之间的传染,可以通过与患者的密切接触进行传染.我们把与患者有过密切接触的人群称为密切接触者,每位密切接触者被感染后即被称为患者.已知每位密切接触者在接触一个患者后被感染的概率为![]() ,某位患者在隔离之前,每天有
,某位患者在隔离之前,每天有![]() 位密切接触者,其中被感染的人数为
位密切接触者,其中被感染的人数为![]() ,假设每位密切接触者不再接触其他患者.
,假设每位密切接触者不再接触其他患者.
(1)求一天内被感染人数为![]() 的概率
的概率![]() 与
与![]() 、
、![]() 的关系式和
的关系式和![]() 的数学期望;
的数学期望;
(2)该病毒在进入人体后有14天的潜伏期,在这14天的潜伏期内患者无任何症状,为病毒传播的最佳时间,设每位患者在被感染后的第二天又有![]() 位密切接触者,从某一名患者被感染,按第1天算起,第
位密切接触者,从某一名患者被感染,按第1天算起,第![]() 天新增患者的数学期望记为
天新增患者的数学期望记为![]() .
.
(i)求数列![]() 的通项公式,并证明数列
的通项公式,并证明数列![]() 为等比数列;
为等比数列;
(ii)若戴口罩能降低每位密切接触者患病概率,降低后的患病概率![]() ,当
,当![]() 取最大值时,计算此时
取最大值时,计算此时![]() 所对应的
所对应的![]() 值和此时
值和此时![]() 对应的
对应的![]() 值,根据计算结果说明戴口罩的必要性.(取
值,根据计算结果说明戴口罩的必要性.(取![]() )
)
(结果保留整数,参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴非负半轴为极轴建立极坐标系,点
轴非负半轴为极轴建立极坐标系,点![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 在线段
在线段![]() 的延长线上,且满足
的延长线上,且满足![]() ,点
,点![]() 的轨迹为
的轨迹为![]() .
.
(1)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)设点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 面积的最小值。
面积的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 是圆柱
是圆柱![]() 底面圆O的直径,底面半径
底面圆O的直径,底面半径![]() ,圆柱的表面积为
,圆柱的表面积为![]() ,点
,点![]() 在底面圆
在底面圆![]() 上,且直线
上,且直线![]() 与下底面所成的角的大小为
与下底面所成的角的大小为![]() .
.
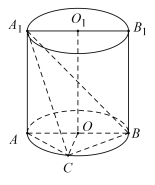
(1)求![]() 的长;
的长;
(2)求二面角![]() 的大小的余弦值.
的大小的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com